
相关文档
Introduction
- 3DGS由于无序性和不规则性,使其无法准确的获得场景的几何表面信息。并且3DGS只关注图像重建的loss,而没有考虑到几何重建的loss。
- 本文的作者提出了一种深度的无偏估计方法以获取更准确的深度值。之前的方法是在相机坐标系的z方向上,对每个高斯分布做累加得到深度值,这会导致深度对应曲面的问题,如图2所示。3DGS是一个椭球,深度做累积的话,得到的深度是一个曲面,而不是一个平面。

- 为解决这个问题,作者将3D高斯压缩成平面,并得到高斯平面的法向量和相机到平面的距离。通过将二者相除,可以得到相机光线和高斯平面的交点,改点到相机的距离为真正的深度值。
- 除此之外,还引入了单视角和多视角的正则项来优化每个像素的平面参数。
- 单视角正则项是假设相邻像素通常属于同一个平面。所以可以从相邻像素的深度中估计法向量并与当前像素的法向量保持一致。(在图像边缘处这个假设通常不成立,因此需要做边缘检测并把这部分区域的权重降低)
- 多视角正则项是确保在不同视角下的几何一致性。具体实现后文会提到。
- 最后,作者还引入两个光度系数来补偿图像中的光照变化,进一步提高重建质量。
Method
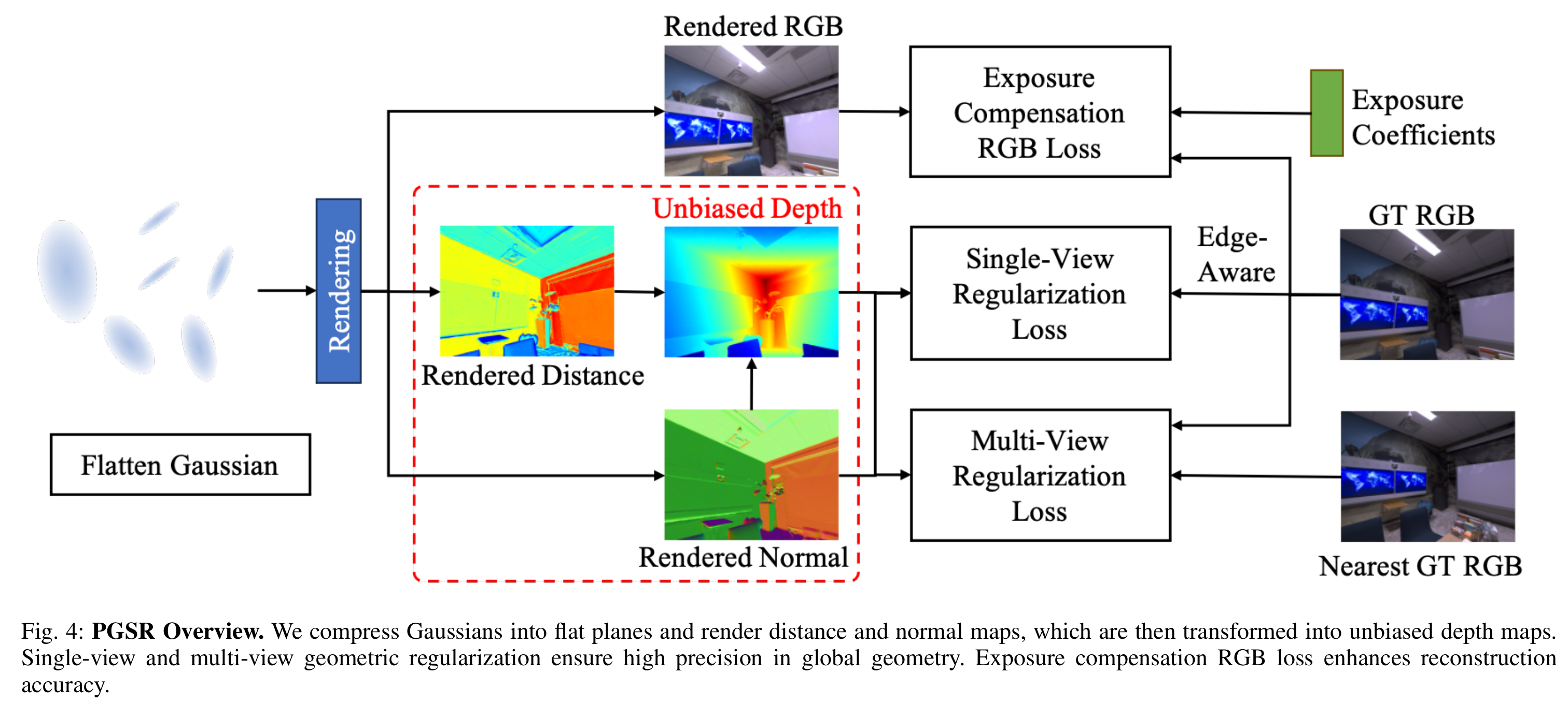
Planar-based Gaussian Splatting Representation
- Flattening 3D Gaussian
- 原始的3D高斯的协方差矩阵为 Σi=RiSiSiTRiT,其中 Ri 表示椭球三个方向的正交基,Si 为沿着三个方向的尺度。这里把椭球压缩成平面,就是把椭球沿着最小尺度的方向压缩,也就是把这个最小的scale作为了loss中的一项:
Ls=∣∣min(s1,s2,s3)∣∣1
- Unbiased Depth Rendering
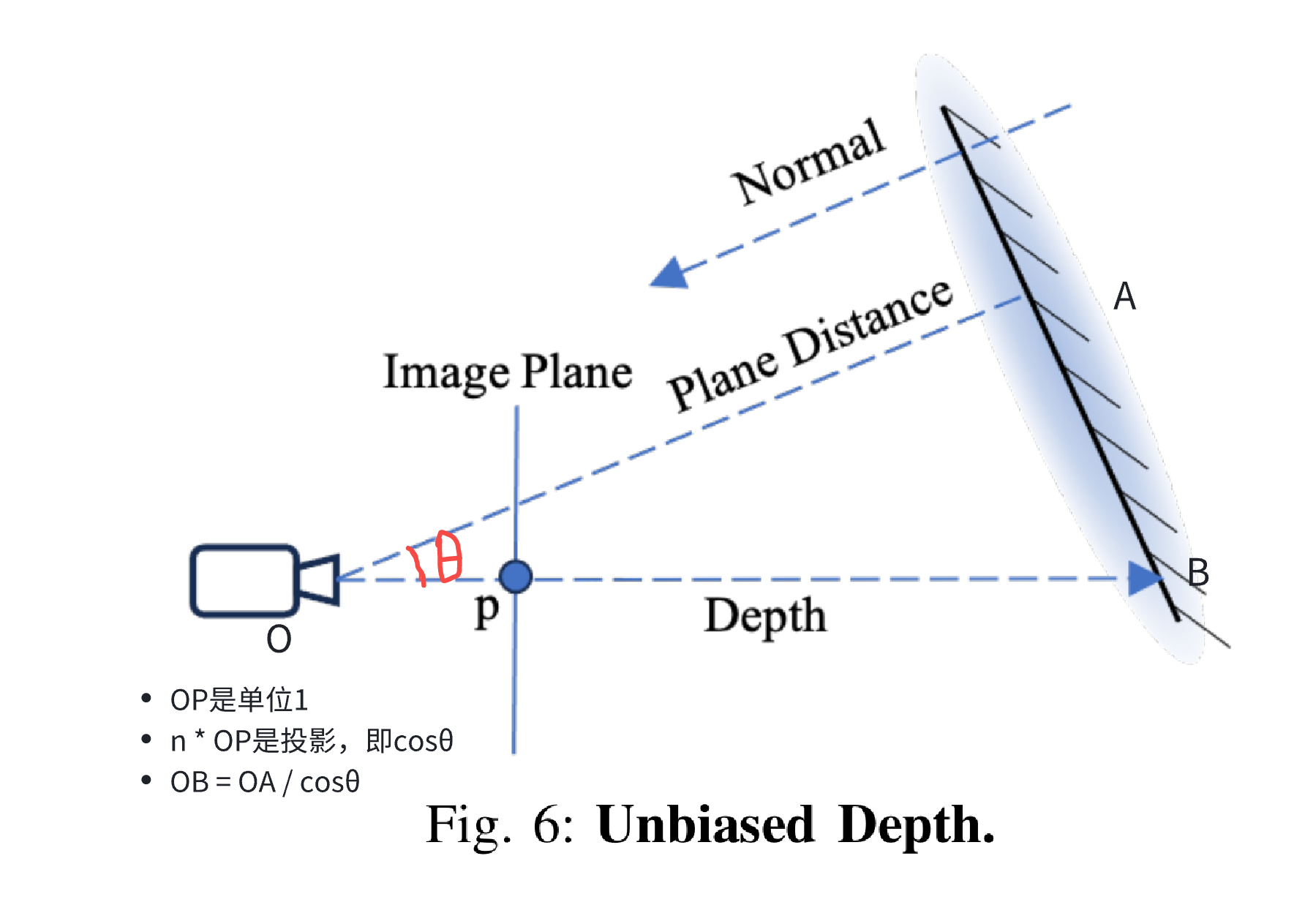
- 取scale最小的方向 ni 作为平面法向量,利用相机到global坐标系的旋转变换 Rc 变换到相机坐标系下,并利用 α-blending的方法,得到当前像素所有高斯的整体法向量:
N=i∈N∑RcTniαij=1∏i−1(1−αj)
- 每个高斯核到相机的距离为 di=(RcT(μi−Tc))T(RcTni),其中 Tc为相机中心在世界坐标系下的位置,μi 为高斯核的世界坐标系下的位置。再次利用 α-blending的方法,得到当前像素所有高斯的整体深度:
D=i∈N∑diαij=1∏i−1(1−αj)
- 得到法向量N和D后,利用下式得到交点到相机的距离,即为真正的深度值:
D(p)=N(p)K−1p~D
- 其中 K 为相机内参,p~为归一化后的像素坐标。
- 这样计算深度的方法有两个好处:
- 这种深度和高斯平面一致,以前的方法是基于高斯的Z做α=blending,因此深度是曲面。
- 由于每条射线的累积权重可能小于1,以前的渲染方法受到权重累积的影响,可能导致深度更靠近相机侧。相比之下,本文的深度是通过将渲染原点到平面的距离除以法线得到的,有效地消除了权重累积系数的影响。
Geometric Regularization
- Single-view Regularization
- 局部平面性假设:一个像素及其相邻像素可以被视为一个近似平面。渲染深度图后,四个相邻点进行采样。利用它们的深度计算平面的法线。然后,最小化此法线图与渲染的法线图之间的差异,确保局部深度和法线之间的几何一致性。
- 对于每个像素,取其四个相邻像素,并拿到相机坐标系下其对应的3D点 {Pj∣j=1,...,4},并计算它们对应平面的法向量:
Nd(p)=∣(P1−P0)×(P3−P2)∣(P1−P0)×(P3−P2)
Lsvgeom =W1p∈W∑(1−∇I)2∥Nd(p)−N(p)∥1
其中 ∇I 为归一化之后的图像梯度,范围在0到1之间,用以控制边缘区域的权重。
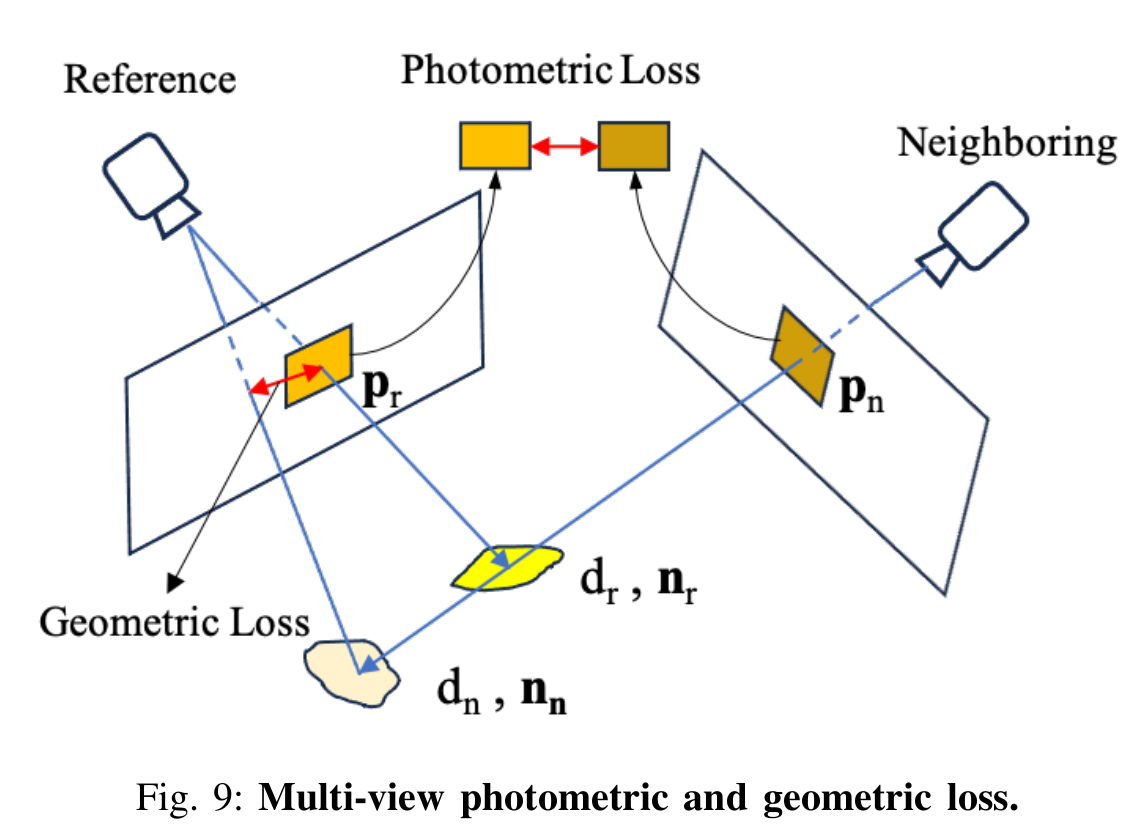
- Multi-View Geometric Consistency
- 如下图所示,对于关键帧和相邻帧,分别渲染法向量和相机到平面的距离。对于关键帧中的特定像素 pr,其对应法向量为nr,距离为dr。关键帧中的像素 pr 可以通过单应矩阵 Hrn 投影到相邻帧中的像素 pn。
Hrn=Kn(Rrn−drTrnntT)Kr−1
- 此时计算出重投影误差,即可作为多视角几何一致性loss:
Lmvgeom=V1pr∈W∑ω(pr)ϕ(pr)ϕ(pr)=∣∣pr−HnrHrnpr∣∣w(pr)={1/exp(ϕ(pr)),0, if ϕ(pr)<1 if ϕ(pr)>=1
其中ω(pr)表示权重,如果两次重投影误差太大,则可能是有遮挡,此时就降低该权重。
-
Multi-View Photometric Consistency
- 从MVS中获得灵感,作者取像素周围7x7的像素块,将其映射到相邻帧中,并将其转换成灰度图,使用NCC(normalized cross correlation)计算两个patch之间的光度误差作为一个loss项:
Lmvrgb=V1pr∈W∑w(pr)(1−NCC(Ir(pr),In(Hrnpr)))
-
Geometric Regularization Loss
Lgeom=λ2Lsvgeom+λ3Lmvrgb+λ4Lmvgeom
Exposure Compensation Image Loss
- 作者认为,之前3DGS没考虑光照变化,因此在实际场景中会出现浮动的噪点。作者为每个图像添加两个曝光系数a,b,用这两个系数可以计算出有曝光补偿的图像:
Iia=exp(ai)Iir+bi
- 对应的loss如下:
Lrgb=(1−λ)L1(I~−Ii)+λLSSIM(Iir−Ii).I~={Iia,Iir, if LSSIM(Iir−Ii)<0.5 if LSSIM(Iir−Ii)>=0.5
- 其中 Ii 为真实图像。
Experiment
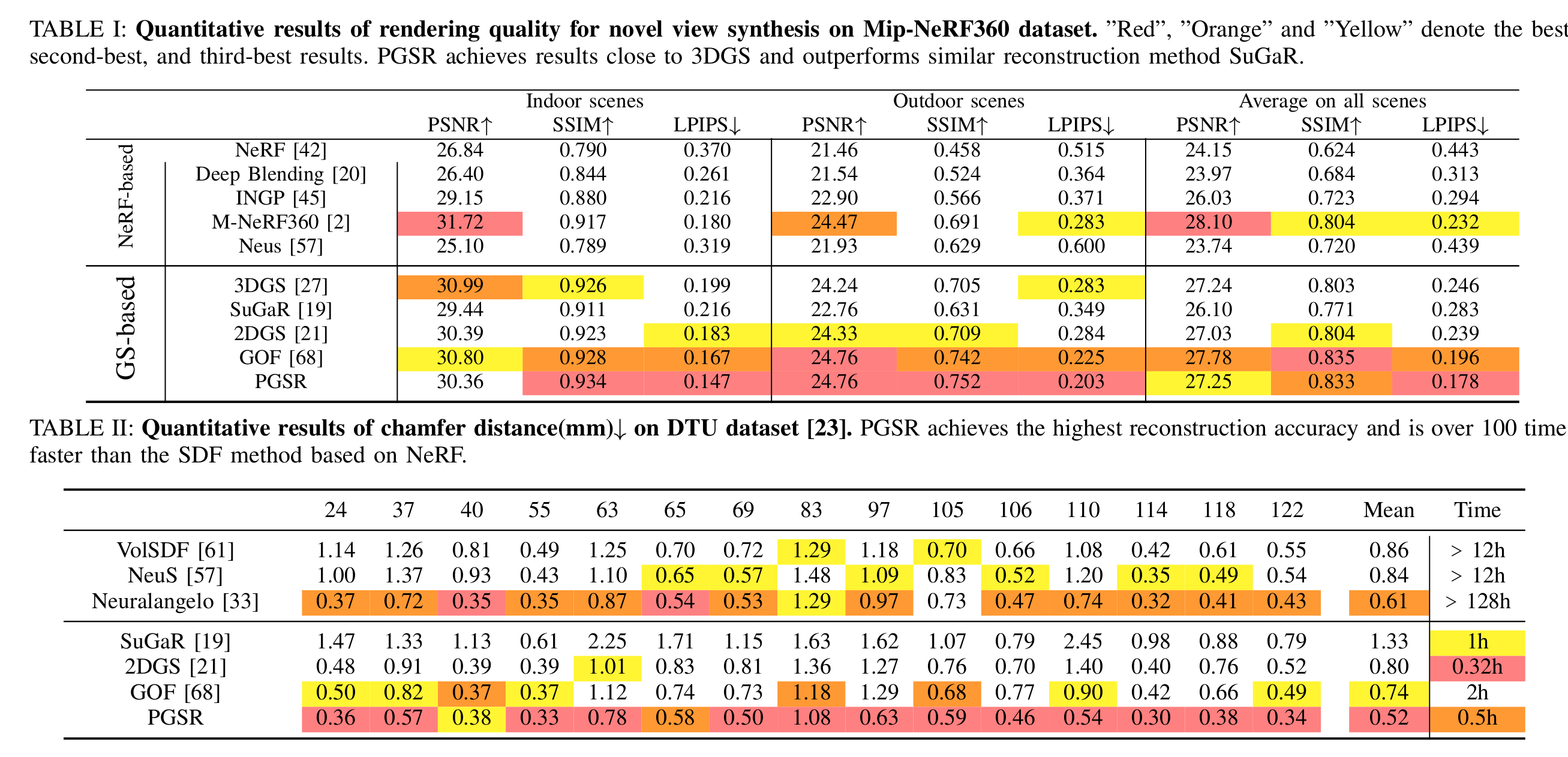


实测数据









