HQSR-GS阅读笔记（压扁3DGS使其更好重建物体几何信息）

相关文档

• 项目链接：https://turandai.github.io/projects/gaussian_surfels/
• 代码链接：https://github.com/turandai/gaussian_surfels
• 论文链接：https://arxiv.org/pdf/2404.17774
• 视频介绍：https://www.bilibili.com/video/BV1uMwveGEiY/?spm_id_from=333.1391.0.0&vd_source=9629687338410a5ccaa5e1a595d0f17d

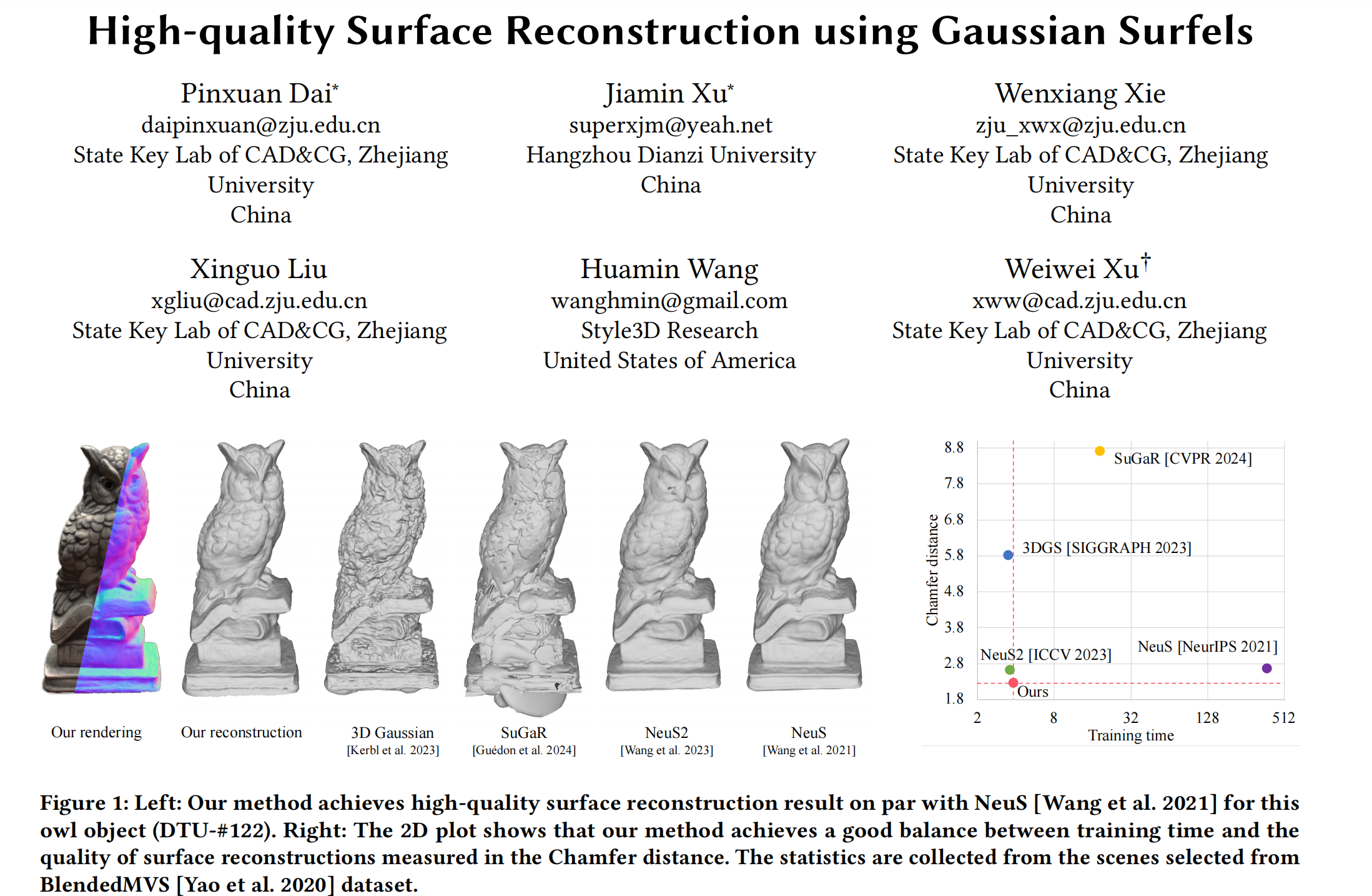
Introduction

• 开头经典介绍3DGS的优势：显示表达；可以动态添加和删除3DGS点，对高频细节有比较好的表达效果；使用GPU/CUDA在渲染的光栅化步骤做了加速，大幅缩短了训练和渲染时间
• 作者认为目前3DGS还有3个方面的不足：
  • 高斯椭球的厚度非零：3DGS是用3D椭球体作为基础单元，但它在每个轴都有厚度，因此无法和实际表面有紧密的贴合；（SuGaR和NeuSG都引入了正则化项来最小化每个轴的缩放因子尺度来缓解这个问题）
  • 法线方向的歧义性：法线轴在优化过程中会随着不同的尺度方向变化，这个模糊性可能导致在重建精细细节的几何信息时不准确；
  • 建模尖锐的表面边缘：当出现3DGS超过表面边缘或距离边缘很远时，$\alpha$ blending过程会给重建的边缘表面引入噪声。
• 本文作者提出一种新的表达：Gaussian surfels，同时结合了3DGS的优化灵活性和面元表面的排列特性，借此提高了重建后的几何质量。主要的实现方法为直接设置3DGS的scale矩阵的z-scale为0。这样的方式可以在优化的过程中，非常明确的把z轴当作法向量，以此来提高优化的稳定性和表面的贴合程度。
• 这种方法会导致计算协方差矩阵时，相对于局部z轴的导数会为0，因此计算的RGB-Loss无法传播到z轴上来，导致该维度的数据永远不会优化。因此作者提出一种自监督的法向量-深度一致性的loss来避免z轴不优化的问题，主要做法为：要求局部z轴尽可能贴合高斯重建后的深度图计算出来的法向量。
• 另外一个主要的改进，是调整3DGS中截断的阈值。并提出了一种体积切割方法，根据高斯体素到面元的距离来决定一个是否应该切割。

Method

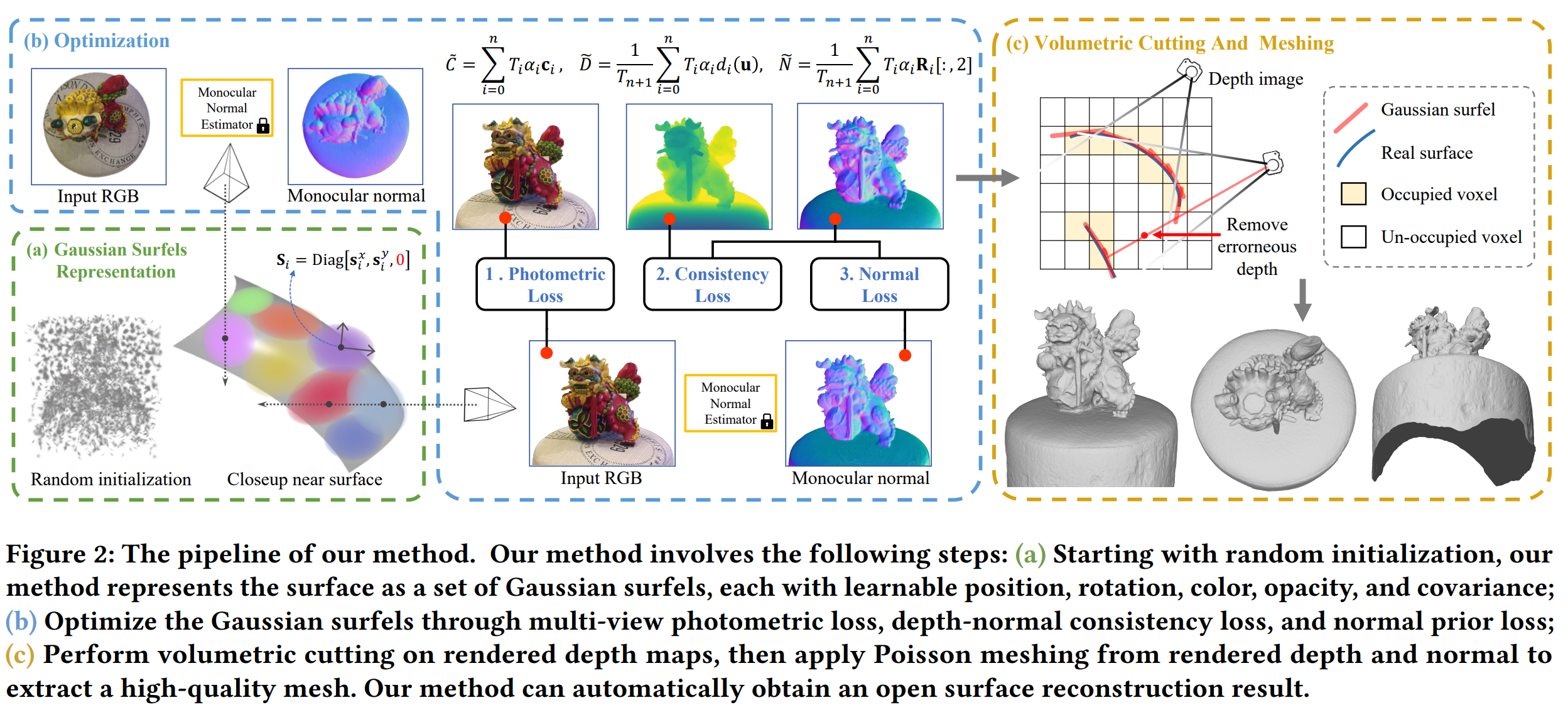
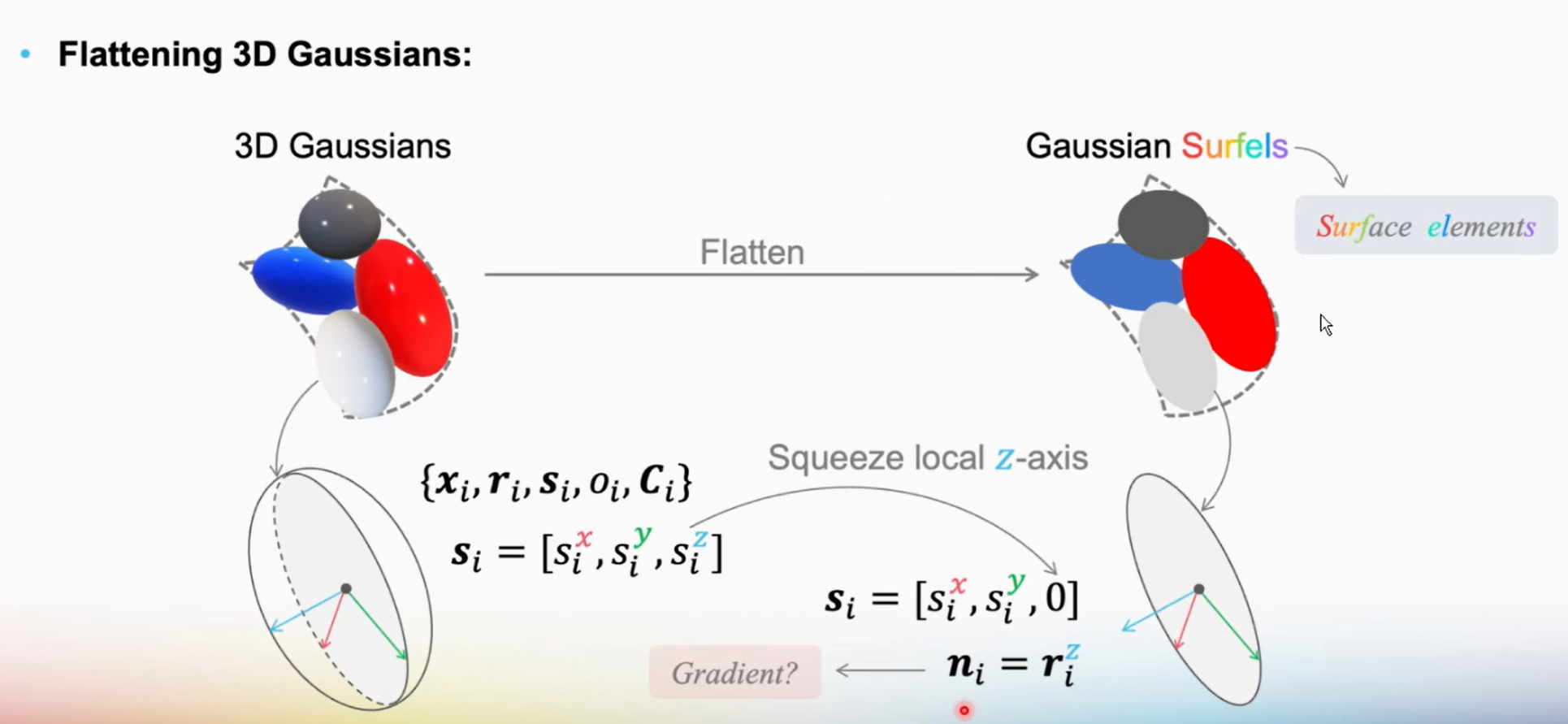
高斯面元

• 每个高斯面元可以表示为$\left\{ \mathbf{x}_i, \mathbf{r}_i, \mathbf{s}_i, \mathbb{o}_i, \mathcal{C}_i\right\}_{i\in\mathcal{P}}$，一个高斯分布可以表示为：

$$G(\mathbf{x}; \mathbf{x}_i, \Sigma_i) = \exp\left\{-0.5(\mathbf{x} - \mathbf{x}_i)^T\Sigma_i^{-1}(\mathbf{x} - \mathbf{x}_i)\right\}$$

• 作者这里把尺度向量设置为：$\mathbf{s}_i = [s_i^x, s_i^y, 0]^T$来将3D椭球压缩为2D的面元，因此对应的协方差矩阵就变为了：

  $$\Sigma_i = \mathbf{R}(\mathbf{r}_i)\mathbf{S}_i\mathbf{S}_i^T\mathbf{R}(\mathbf{r}_i)^T \\ =\mathbf{R}(\mathbf{r}_i)_i^T\left[{(s_i^x)}^2, {(s_i^y)}^2, 0\right]\mathbf{R}(\mathbf{r}_i)^T$$

• 这样的表示形式，可以很轻松的把每个3D高斯椭球转变成2D的椭圆面，并且每个椭圆面的法向量可以直接从旋转矩阵中提取出来：$\mathbf{n}_i = \mathbf{R}(\mathbf{r}_i)[:, 2]$。这种方法就可以直接优化面元的法向量尽可能的贴合实际物体表面的法向量。

• 对于深度和法向量的计算，也是类似于每个像素的颜色值计算的$\alpha$-blending过程：

  $$\tilde{N} = \frac{1}{1-T_{n+1}}\sum_{i=0}^n T_i\alpha_iR_i[:, 2], \tilde{D} = \frac{1}{1-T_{n+1}}\sum_{i=0}^n T_i\alpha_id_i(\mathbf{u})$$

  • 其中，$\alpha_i = G'(\mathbf{u}; \mathbf{u}_i, \Sigma_i')\mathbf{o}_i$代表每个高斯核的权重，$T_i = \prod_{j=0}^{i-1}(1-\alpha_i)$这里使用$\frac{1}{1+T_{n+1}}$来对渲染的权重$T_i\alpha_i$进行归一化，在颜色渲染时，是添加了一个背景颜色来影响像素的颜色值，而对于深度和法向量的渲染则直接采用这种归一化的方法，作者认为这种方法更适合深度和normal。
• 在深度渲染时，之前3DGS的深度都是按照中心点计算的，由于其有一定的体积，因此该方法无法准确的计算深度，而作者压缩为2D平面后，可以精确的计算出每个ray和2D面元精确的交点在什么位置，这样计算出来的深度值会更准确，计算公式为：

  $$d_i(\mathbf{u}) = d_i(\mathbf{u}_i) + (\mathbf{W}_k\mathbf{R}_i)[2, :]\mathbf{J}_{pr}^{-1}(\mathbf{u}-\mathbf{u}_i)$$

  • 其中$\mathbf{J}_{pr}^{-1}$代表把像素从图像平面映射到高斯面元的切面的雅可比的逆，$(\mathbf{W}_k\mathbf{R}_i)$表示将高斯面元的旋转矩阵变换到相机空间中。

优化

• 整个优化过程共包含5个loss项

  $$\mathcal{L} = \mathcal{L}_p + \mathcal{L}_n + \lambda_o\mathcal{L}_o+ \lambda_c\mathcal{L}_c+\lambda_m\mathcal{L}_m$$

• 分别为：
  • RGB的loss $\mathcal{L}_p$
  • 法向量先验的loss $\mathcal{L}_n$
  • 不透明度loss $\mathcal{L}_o$
  • 深度-法向量一致性loss $\mathcal{L}_c$
  • Mask loss $\mathcal{L}_m$（计算语义分割的交叉熵loss）

Photometric loss$\mathcal{L}_p$

• 计算渲染后图像和gt图像的L1 loss和D-SSIM两部分组成：

  $$\mathcal{L}_p = 0.8 \cdot L_1(\tilde{\mathbf{I}}, \mathbf{I}) + 0.2\cdot L_{DSSIM}(\tilde{\mathbf{I}}, \mathbf{I})$$

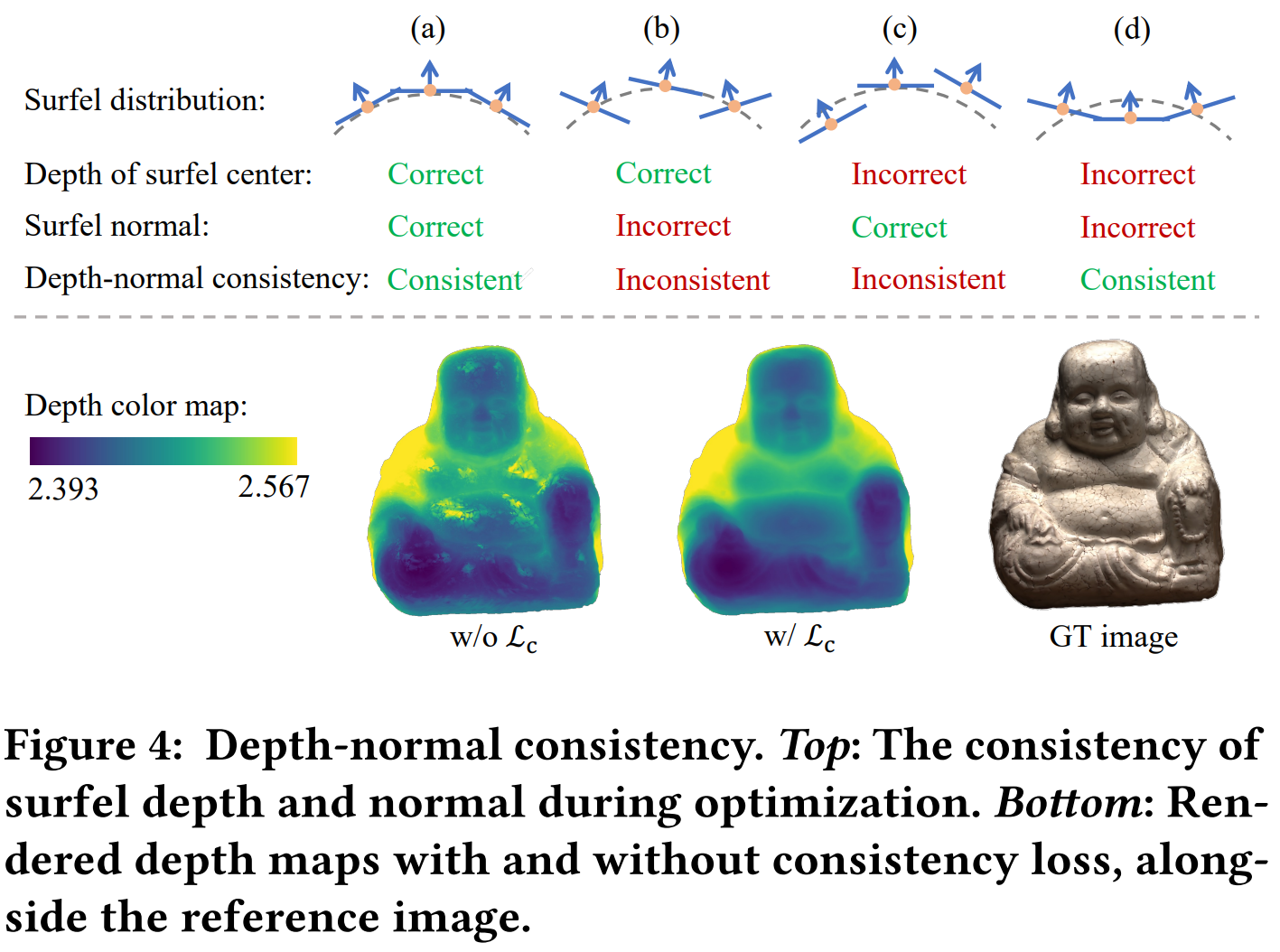
Depth-normal consistency loss$\mathcal{L}_c$深度-法向一致性loss

• 这里是将渲染后的深度和法向量做了关联：

  $$\mathcal{L}_c = 1 - \tilde{\mathbf{N}} \cdot N(V(\tilde{\mathbf{D}}))$$

  • 这里$V(\cdot)$是将每个像素的深度转成一个3D点，并用$N(\cdot)$取其最近邻的点计算法向量。**作者认为这里的一致性loss在整个优化的过程中是很重要的一个loss，尤其是在解决每个高斯面元的梯度消失的问题。**这里是因为z轴的尺度置零，因此z轴的法向量无法得到更新才会出现梯度消失的问题。
  • 除此之外，这种一致性loss还可以互相监督：

Normal-prior loss$\mathcal{L}_n$

• 这个loss用于在有高光的场景确保深度信息不会被RGB的loss影响到。共包含两个部分：
  • 渲染后的法相和prior的法相的loss和渲染后的法相的梯度为0。

  $$\mathcal{L}_n = 0.04 \cdot (1 - \mathbf{\tilde{N}} \cdot \mathbf{\hat{N}}) + 0.005 \cdot L_1(\nabla \mathbf{\tilde{N}}, \mathbf{0} )$$

Opacity loss$\mathcal{L}_o$

• 鼓励每个高斯面元的不透明度接近0或者1。这个loss在4DrotorGS中也有提到，可以减少漂浮物。

  $$\mathcal{L}_o = exp(-(o_i - 0.5)^2 / 0.005)$$

Gaussian Point Cutting and Meshing

• 当高斯面元超过真实表面边缘时，背景的深度值会被前景的这部分影响到，见下图：

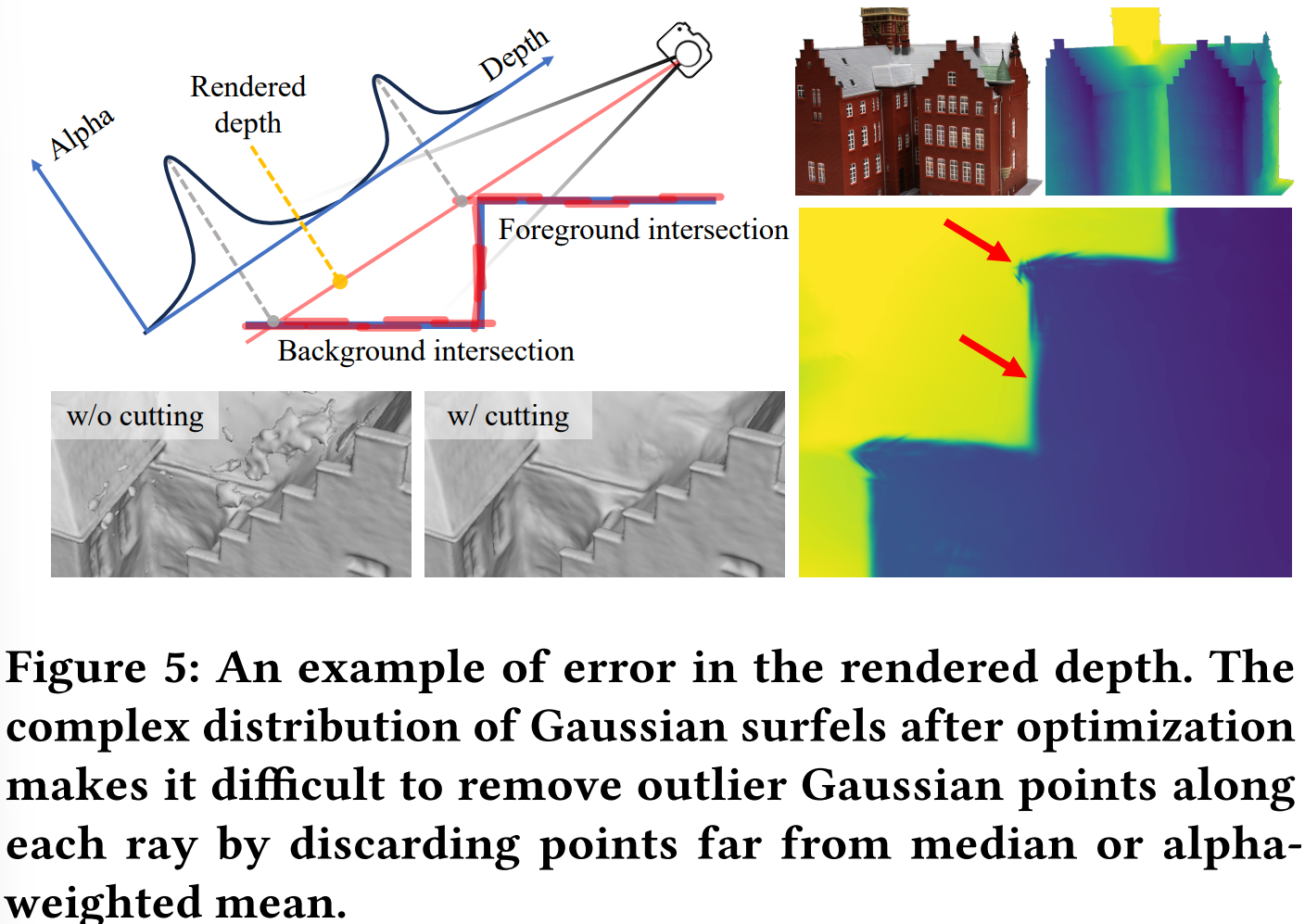
• 针对这个问题，作者提出了对每个高斯面元聚合alpha值来实现体素切割。首先在bbox中分割出$512^3$的体素栅格，然后遍历所有的高斯面元，计算与其相交的体素的不透明度并累加，如果栅格有比较低的累加值，则删掉这个体素。

Experiments