4DRotorGS阅读笔记（Rotor表示4D空间旋转的动态场景重建方法）

相关文档

Introduction

  • 当前的 3D 场景重建主要分为静态和动态两种场景，动态场景由于物体运动的原因，导致 NVS 的效果都比较差。
  • 目前一些方法会把 3D 场景和它的动态变化一起建模，但这样很复杂，会由于高度纠缠的空间&时间维度，导致 NVS 的细节很差。
  • 还有一些方法是把动态和静态空间解耦，先构建一个静态的规范空间，然后预测一个变形场来表示动态变化。但这种方法对于物体突然出现和突然消失的情况仍然不适用。
  • 作者提出方法的时期，针对动态场景的重建，主要都是 NeRF-Based 的方法，要用大量的 ray 实现渲染，无法满足实时性。
  • 本文的主要是在 3dgs 的基础上，将场景从 3D 扩展成 4D。核心思想是，每一个 t 时刻的 3D 场景，可以当做是 4D 时空椭球在 t 时刻的切面。以下图所示：

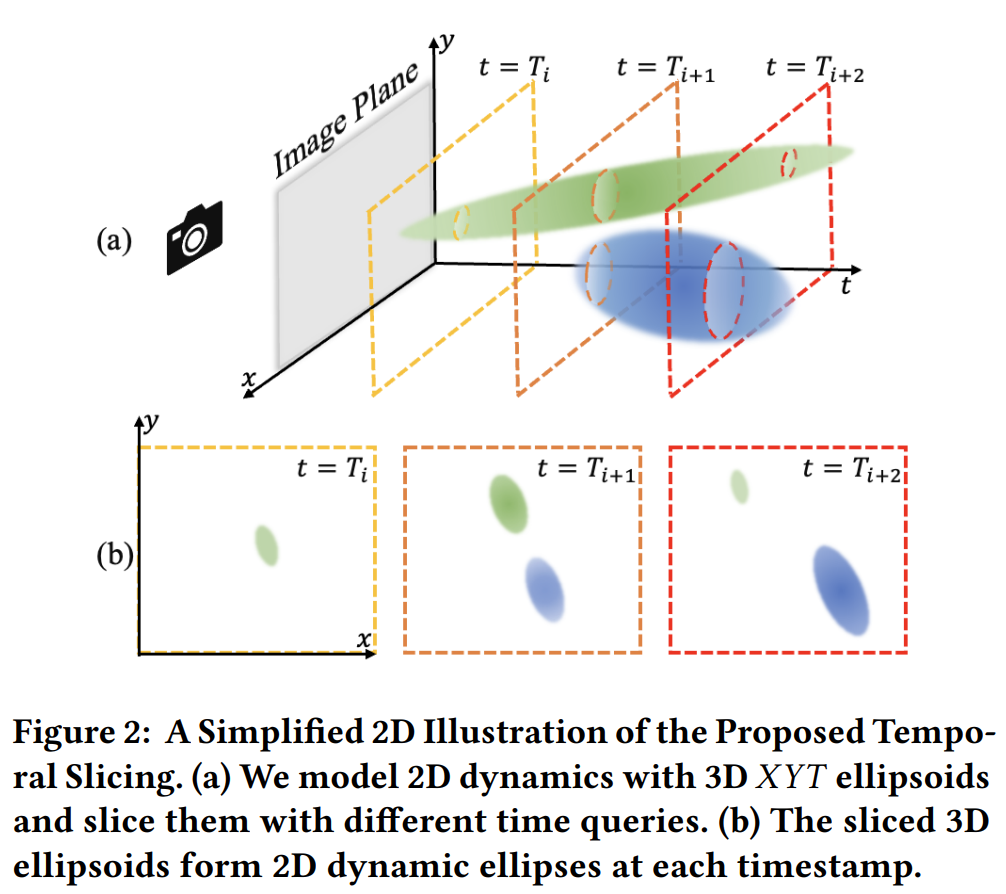
  • 图中展示的是 3D 切 2D 的情况，4D 切 3D 也类似，每个 t 时刻，切出来的就是一组 3D 的椭球，这样再继续往 2d 上投影，就和单帧的 3dgs 一样了。并且这样的建模方式，可以很好的解决物体突然出现和突然消失的问题。
  • 作者使用𝑁-Dimensional Rigid Body Dynamics中的方法描述 4D 的旋转，同时如果把时间维度置零，这个 4D 的旋转就和 3D 维空间的旋转是一样的了，这样就和 3DGS 没什么区别。因此本文既可以用于动态的 4D 空间重建，也可以用于静态的 3D 空间重建。
  • 文章还额外提出两种新的正则化项：
    • 熵损失，推动高斯球的不透明度更趋向于 0 或者 1，这样可以有效的减少重建后的“漂浮物”
    • 4D 一致性 loss，规范高斯的运动，并产生一致的动态重建

Method

3DGS

  • 3DGS 用 N 个各向异性的 3D 高斯椭球体来建模一个静态场景。每个椭球体用自身的协方差矩阵Σ\Sigma和中心点μ\bold{\mu}表示：

    G(x)=e−12(x−μ)TΣ−1(x−μ)G(\boldsymbol{x}) = e^{-\frac{1}{2}(\boldsymbol{x}-\bold{\mu})^T\Sigma^{-1}(\boldsymbol{x}-\bold{\mu})}

  • 为了确保优化过程中协方差矩阵半正定有效，Σ\Sigma被分解为缩放矩阵S\bold{S}和旋转矩阵R\bold{R}来表征椭球体的形状：

    Σ=RSSTR\Sigma = \bold{R}\bold{S}\bold{S}^T\bold{R}

    其中S=diag(sx,sy,sz)∈R3\bold{S} = diag(s_x, s_y, s_z) \in \mathbb{R}^{3}, R∈SO(3)\bold{R} \in SO(3)。除此之外，每个高斯椭球体还有一些可学习的参数，例如不透明度o∈(0,1)o \in (0, 1)，k 阶的球谐系数表征颜色。

  • 3DGS 投影到 2D 平面上时，是计算相机空间的协方差矩阵Σ′=JVΣJTVT\Sigma^{'} = \boldsymbol{J}\boldsymbol{V}\Sigma\boldsymbol{J}^T\boldsymbol{V}^T。其中J\boldsymbol{J}是仿射变换的近似雅可比，V\boldsymbol{V}是相机空间到世界空间的变换矩阵。然后根据高斯球距离相机平面的距离，按照 depth 进行排序距离越近越先投影。

C=∑i=1Nciαi∏j=1i−1(1−αj)C=\sum_{i=1}^{N}c_i\alpha_i\prod_{j=1}^{i-1}(1-\alpha_j)

其中cic_i是第ii个高斯球的颜色，αi=oiG′\alpha_i = o_iG'是第ii个高斯球的不透明度和 2D 投影结果的乘积。

4DGS

  • 整体框架如下图所示：

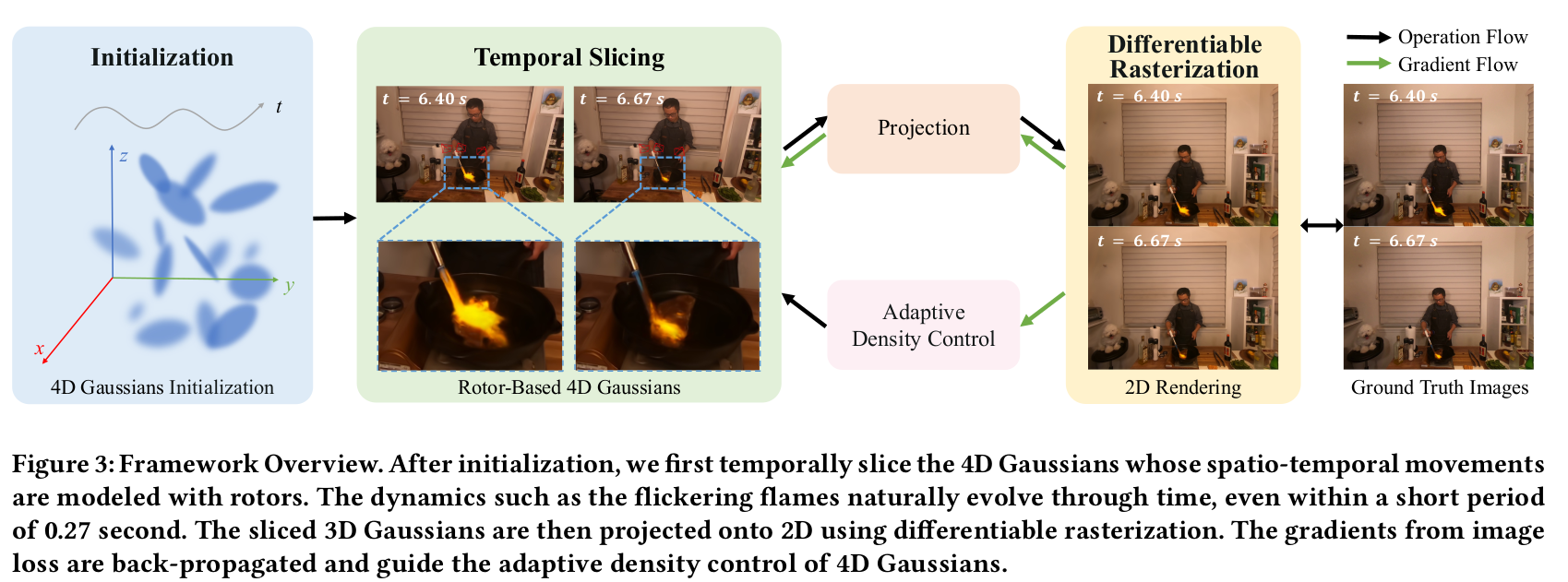
Rotor-Based 的 4DGS 表示

  • 类似于 3DGS，4DGS 也可以用一个 4 维的中心点μ4D=(μx,μy,μz,μt)\boldsymbol{\mu}_{4D} = (\mu_x, \mu_y, \mu_z, \mu_t)以及一个 4D 的协方差矩阵Σ4D\Sigma_{4D}来表示

G4D(x)=e−12(x−μ4D)TΣ4D−1(x−μ4D)G_{4D}(\boldsymbol{x}) = e^{-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu}_{4D})^T\Sigma_{4D}^{-1}(\boldsymbol{x}-\boldsymbol{\mu}_{4D})}

  • 同时，协方差矩阵Σ4D\Sigma_{4D}也可以用 4D 的缩放矩阵S4D\bold{S}_{4D}和 4D 的旋转矩阵R4D\bold{R}_{4D}表示：

    Σ4D=R4DS4DS4DTR4D\Sigma_{4D} = \bold{R}_{4D}\bold{S}_{4D}\bold{S}_{4D}^T\bold{R}_{4D}

    其中S4D=diag(sx,sy,sz,st)\bold{S}_{4D} = diag(s_x, s_y, s_z, s_t)的表示形式比较简单，但是**如何描述一个 4D 的旋转矩阵R4D\bold{R}_{4D}呢？**参考𝑁-Dimensional Rigid Body Dynamics这篇文章，使用 rotor 描述 4D 的旋转。这里 rotor 由一组 8 个组件组成：

    r=s+b01e01+b02e02+b12e12+b03e03+b13e13+b23e23+pe0123\bold{r} = s + b_{01}\bold{e}_{01} + b_{02}\bold{e}_{02} + b_{12}\bold{e}_{12} + b_{03}\bold{e}_{03} + b_{13}\bold{e}_{13} + b_{23}\bold{e}_{23} + p\bold{e}_{0123}

    其中，$\bold{e}{0123} = \bold{e}{0} \wedge \bold{e}{1} \wedge \bold{e}{2} \wedge \bold{e}_3 $，并且 e_ij=e_i∧e_j\bold{e}\_{ij} = \bold{e}\_i \wedge \bold{e}\_j表示四维欧几里得空间中标准正交基对应的轴之间的外积。因此，4D 的旋转，可以通过 8 个系数确定。

  • 与四元数类似，4D 旋转的 rotor 也可以转换成 4D 的旋转矩阵R4D\bold{R}_{4D}的形式。先对 rotor 进行归一化，然后再映射到 4D 旋转矩阵的形式：

    R4D=Fmap(Fnorm(r))\bold{R}_{4D} = \mathcal{F}_{map}(\mathcal{F}_{norm}(\bold{r}))

  • rotor 的 8 个分量中，前 4 个分量代表 3D 的空间旋转，后 4 个分量代表时空旋转，即空间平移。此时如果把后 4 个分量置零，那就等价于 3D 空间中的 4 元数，那么该方法就可以用于 3D 静态空间的重建。

时间切片的 4DGS

  • 给定 4D 的协方差矩阵Σ4D\Sigma_{4D}和逆矩阵Σ4D−1\Sigma_{4D}^{-1}，其组成为：

    Σ4D=[UVVTW],Σ4D−1=[AMMTZ]\Sigma_{4D} = \begin{bmatrix} U & V \\ V^T & W \end{bmatrix}, \Sigma_{4D}^{-1} = \begin{bmatrix} A & M \\ M^T & Z \end{bmatrix}

  • 此时，给定一个时间tt，对应的 3D 高斯椭球可以表示为：

    G3D(x,t)=e12λ(t−μt)2e−12[x−μ(t)]TΣ3D−1[x−μ(t)]G_{3D}(\boldsymbol{x}, t) = \boldsymbol{e}^{\frac{1}{2}\lambda (t-\mu_t)^2}\boldsymbol{e}^{-\frac{1}{2}[\boldsymbol{x} - \boldsymbol{\mu}(t)]^T \Sigma^{-1}_{3D} [\boldsymbol{x} - \boldsymbol{\mu}(t)]}

其中，

λ=W−1,Σ3D=A−1=U−VVTW,μ(t)=(μx,μy,μz)T+(t−μt)VW\lambda = W^{-1}, \\ \Sigma_{3D} = A^{-1} = U - \frac{VV^T}{W}, \\ \mu(t) = (\mu_x, \mu_y, \mu_z)^T + (t-\mu_t)\frac{V}{W}

  • 和原始的 3DGS 的公式相比，这里多了一个时间衰减项e12λ(t−μt)2\boldsymbol{e}^{\frac{1}{2}\lambda (t-\mu_t)^2}，随着时间 t 推移，当 t 足够接近时间位置μt\mu_t时，高斯点首先出现，并开始增长，当t=μtt = \mu_t时，不透明度达到峰值，之后三维高斯密度逐渐缩小，直到 t 距离μt\mu_t足够远。

  • 除此之外，切片的 3DGS 在高斯的中心位置μx,μy,μz\mu_x, \mu_y, \mu_z上增加了一个运动项(t−μt)VW(t -\mu_t)\frac{V}{W}。从理论上来说，三维高斯函数的线性运动来自于 4D 的切片，并且假设在很小的时间范围内，运动可以近似为线性运动。这样就可以把这个运动拆解为两部分t−μtt-\mu_t为时间，VW\frac{V}{W}为速度。将其可视化后，即可得到每个时刻下，每个部分的运动场（速度场）。

优化

  • 额外引入了两个 loss

Entropy Loss 交叉熵 loss

  • 期望每个高斯椭球的不透明度都接近于 1 或者 0，因此引入了一个交叉熵 loss，使得噪声的不透明度都趋近于 0，避免了“漂浮物”的出现。

    Lentropy=1N∑i=1N−oilog(oi)L_{entropy} = \frac{1}{N}\sum_{i=1}^{N}-o_ilog(o_i)

4D 一致性 loss

  • 在 4D 空间中，高斯的运动应该和附近的点的运动是类似的，因此作者额外引入了一个一致性 loss，对于 t 时刻下的每个高斯点，选择其附近的 K 个最近邻的高斯点，计算其运动的均值，并与当前高斯点的运动进行比较，计算 L1 loss。（注意，这里计算的最近邻点是在 4D 空间中计算的欧氏距离，而不是 3D 空间）

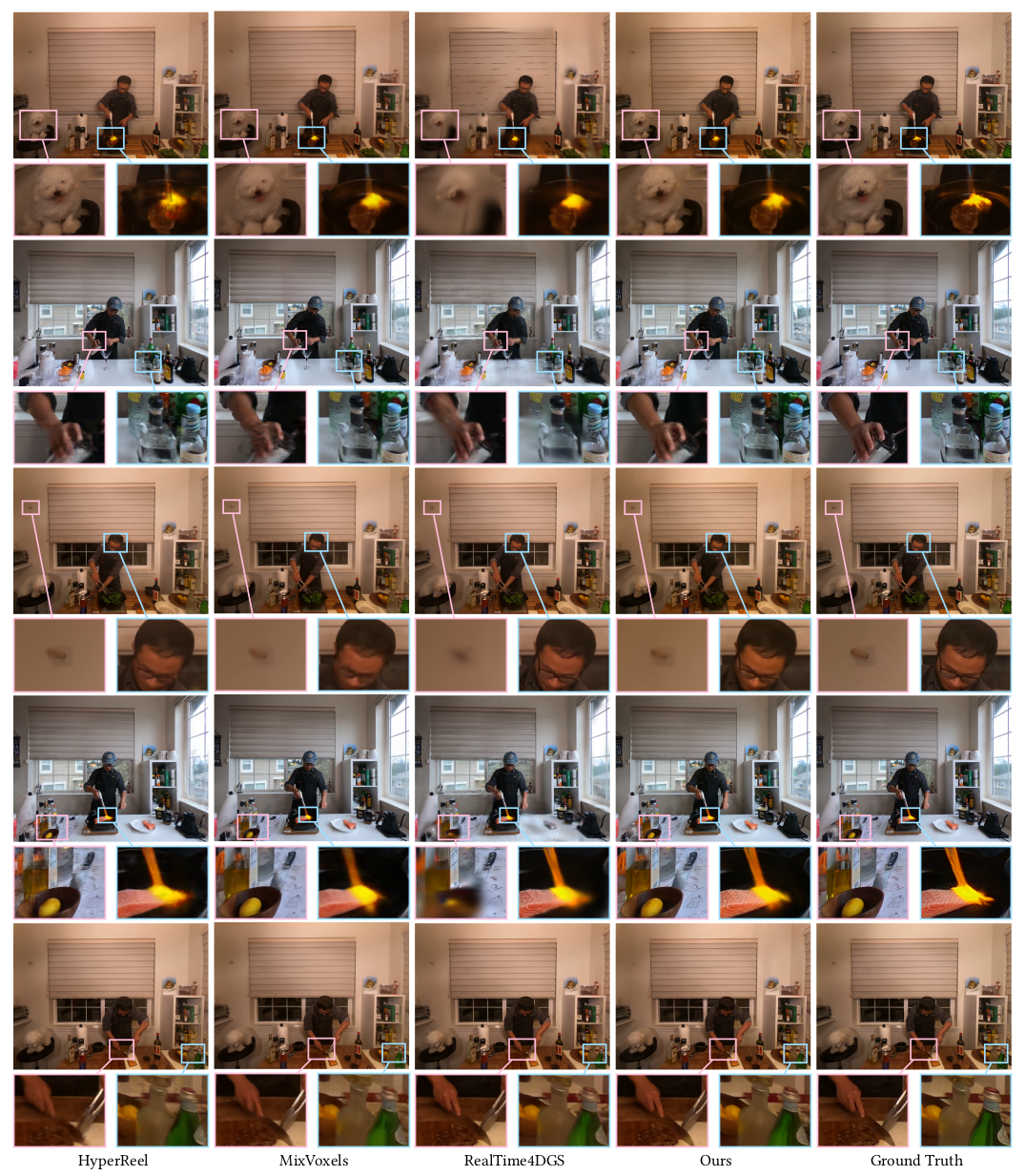
    Lconsistant4D=1N∑i=1N∣∣si−1K∑j∈Ωisj∣∣1L_{consistant4D} = \frac{1}{N}\sum_{i=1}^{N} ||\bold{s}_i - \frac{1}{K}\sum_{j\in \Omega_i\bold{s}_j}||_1

Experiments

视觉重建
4DRotorGS阅读笔记（Rotor表示4D空间旋转的动态场景重建方法）
https://fansaorz.github.io/2025/01/22/4DRotorGS阅读笔记/
作者
Jiashi Zhang
发布于
2025年1月22日
许可协议