常用上采样方法

上采样

• 上采样主要分为三类：
  • 基于线性插值的方法
  • 深度学习的上采样（转置卷积）
  • Unpooling的方法（只是做各种简单的补零或者扩充操作）

线性插值方法

最近邻插值

• 当图片放大时，缺少的像素用临近像素点进行填充，也就是照搬旁边的像素值，会出现明显的锯齿。
• 举例：

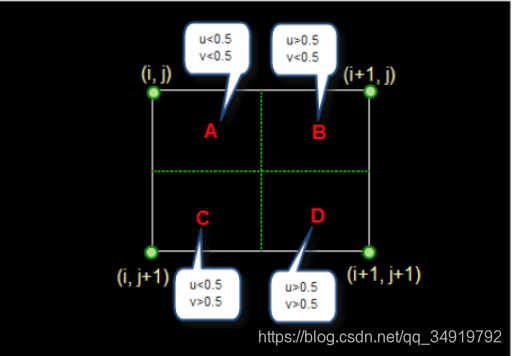
• 如果放大图片后，扩展点位于A区域，则直接用$(i, j)$的像素值填充

双线性插值

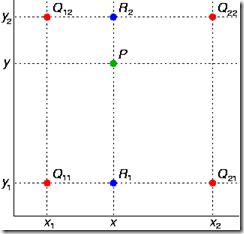
• 根据扩展后像素点的位置，分别在u方向做一次线性插值，在v方向做一次线性插值，最终得到该点像素值。（同时用相邻4个像素的值计算）

$$\begin{align} f(x, y) &\approx \frac{f(Q_{11})}{(x_2-x_1)(y_2-y_1)}(x_2-x)(y_2-y) + \frac{f(Q_{21})}{(x_2-x_1)(y_2-y_1)}(x-x_1)(y_2-y)\nonumber \\ &+ \frac{f(Q_{12})}{(x_2-x_1)(y_2-y_1)}(x_2-x)(y-y_1) + \frac{f(Q_{22})}{(x_2-x_1)(y_2-y_1)}(x-x_1)(y-y_1) \nonumber \end{align}$$

深度学习上采样（转置卷积也叫反卷积）

卷积操作

• 假设有一个4x4的矩阵，卷积核大小为3x3，步长为1，padding为0。如下图所示，输出一个2x2的矩阵。

• 这种卷积操作，是把9个卷积核与输入矩阵进行相乘，得到一个值，多对一的映射关系。

转置卷积操作

• 如果我们要反过来操作，想要把输入矩阵中的一个值映射到输出矩阵的9个值，这是一对多的映射关系。这个就像是卷积操作的反操作。

• 我们可以把一个卷积操作用一个矩阵表示。如下图，是原始的卷积核：

• 我们对这个3x3的卷积核进行重新排列，得到下面这个4x16的矩阵：

• 将输入矩阵转成一个16维的向量，如下图所示：

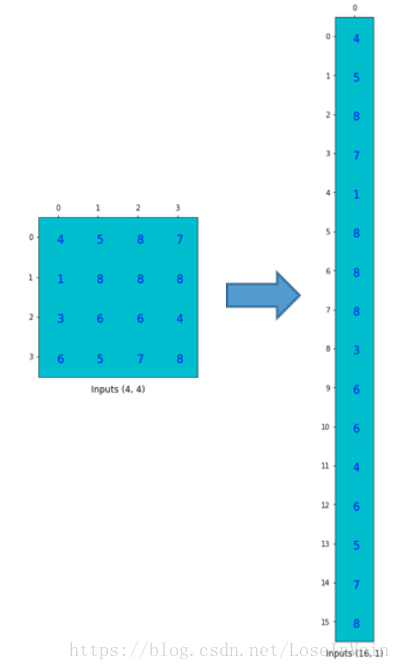
• 将这个4x16的卷积矩阵和1x16的输入向量进行相乘，得到一个4维的列向量：

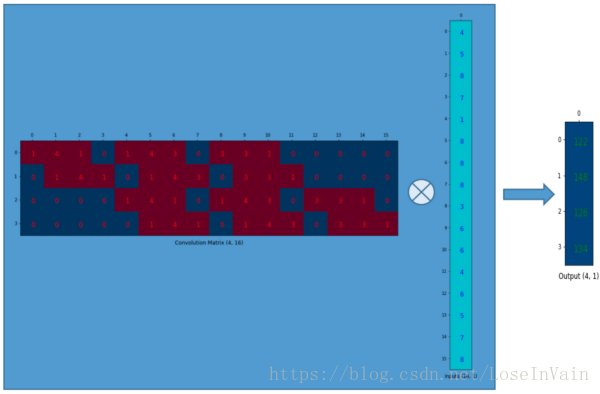
• 这个4维的列向量可以重塑为2x2的矩阵，也就是最开始卷积得到的矩阵。
• 至此，下采样的卷积可以表示为$C_{4\times16} * M_{16\times1} = O_{4\times1} \rightarrow O_{2\times2}$，那么如果把卷积矩阵进行转置，得到一个16x4的矩阵，再与输入向量进行相乘，就可以实现上采样操作。$C_{16\times4} * M_{4\times1} = O_{16\times1} \rightarrow O_{4\times4}$

总结

• 转置卷积操作构建了和普通的卷积操作一样的连接关系，只不过这个是从反向方向开始连接的。我们可以用它进行上采样。另外，这个转置卷积矩阵的参数是可以学习的，因此我们不需要一些人为预先定义的方法。即使它被称为转置卷积，它并不是意味着我们将一些现存的卷积矩阵简单转置并且使用其转置后的值。

• 从本质来说，转置卷积不是一个卷积，但是我们可以将其看成卷积，并且当成卷积这样去用。我们通过在输入矩阵中的元素之间插入0进行补充，从而实现尺寸上采样，然后通过普通的卷积操作就可以产生和转置卷积相同的效果了。你在一些文章中将会发现他们都是这样解释转置卷积的，但是这个因为在卷积操作之前需要通过添加0进行上采样，因此是比较低效率的。

参考文档

• 反卷积和转置卷积
• 关于上采样方法总结（插值和深度学习）
• 一文搞懂反卷积，转置卷积