Loss函数

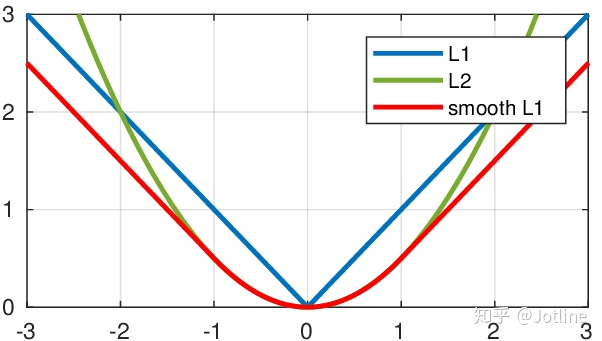
L1 Loss

• L1 Loss，即绝对值误差。
• 公式：

  $$\text{L1Loss}(x, y) =\frac{1}{n}\sum_{i}^{n} |y_i - f(x_i)|$$

• L1 loss在零点不平滑，用的较少。在回归和简单的模型中使用

L2 Loss

• L2 Loss，即均方误差。
• 公式：

  $$\text{L2Loss}(x, y) =\frac{1}{n}\sum_{i}^{n} (y_i - f(x_i))^2$$

• 在回归任务；数值特征不大；问题维度不高时使用

Smooth L1 Loss

• Smooth L1 Loss，即平滑L1损失。

• 公式：

  $$\text{SmoothL1Loss}(x, y) = \begin{cases}0.5(y_i-f(x_i))^2 & if \quad|y_i-f(x_i)| < 1 \\ |y_i - f(x_i)| - 0.5 & otherwise \end{cases}$$

• 平滑版的L1 Loss。仔细观察可以看到，当预测值和ground truth差别较小的时候（绝对值差小于1），其实使用的是L2 Loss；而当差别大的时候，是L1 Loss的平移。Smoooth L1 Loss其实是L2 Loss和L1 Loss的结合，它同时拥有L2 Loss和L1 Loss的部分优点。

• 当预测值和ground truth差别较小的时候（绝对值差小于1），梯度不至于太大。（损失函数相较L1 Loss比较圆滑）

• 当差别大的时候，梯度值足够小（较稳定，不容易梯度爆炸）。

SSIM Loss

• Structural Similarity (SSIM)，即结构相似性。是用来衡量两张图片的质量的一种指标。
• 结构相似度指数从图像组成的角度将结构信息定义为独立于亮度、对比度的反映场景中物体结构的属性，并将失真建模为亮度、对比度和结构三个不同因素的组合。
• 用均值作为亮度的估计，标准差作为对比度的估计，协方差作为结构相似程度的度量。
• 公式：

  $$\text{SSIM}(x, y) = \frac{(2\mu_x\mu_y + c_1)(2\sigma_{xy} + c_2)}{(\mu_x^2 + \mu_y^2 + c_1)(\sigma_x^2 + \sigma_y^2 + c_2)}$$

• Pytorch 计算 SSIM Loss 的代码：

def ssim(img1, img2, window_size=11, size_average=True):
    channel = img1.size(-3)
    window = create_window(window_size, channel)

    if img1.is_cuda:
        window = window.cuda(img1.get_device())
    window = window.type_as(img1)

    return _ssim(img1, img2, window, window_size, channel, size_average)

"""
计算两幅图像的结构相似性指数（SSIM）。

Args:
    img1 (Tensor): 第一幅图像，Tensor类型，形状为[batch_size, channels, height, width]。
    img2 (Tensor): 第二幅图像，Tensor类型，形状为[batch_size, channels, height, width]。
    window (Tensor): 高斯窗函数，Tensor类型，形状为[channels, window_size, window_size]。
    window_size (int): 高斯窗函数的边长。
    channel (int): 图像的通道数。
    size_average (bool, optional): 是否对SSIM值进行平均。默认为True。

Returns:
    Tensor: SSIM值。如果size_average为True，则返回SSIM的平均值；否则，返回每个图像的SSIM值。
"""
def _ssim(img1, img2, window, window_size, channel, size_average=True):
  # 卷积计算局部窗口内的均值
  mu1 = F.conv2d(img1, window, padding=window_size // 2, groups=channel)
  mu2 = F.conv2d(img2, window, padding=window_size // 2, groups=channel)

  mu1_sq = mu1.pow(2)
  mu2_sq = mu2.pow(2)
  mu1_mu2 = mu1 * mu2

  # 计算局部窗口内的标准差
  # \sigma_x^2 = E(x^2) - E(x)^2
  sigma1_sq = F.conv2d(img1 * img1, window, padding=window_size // 2, groups=channel) - mu1_sq
  sigma2_sq = F.conv2d(img2 * img2, window, padding=window_size // 2, groups=channel) - mu2_sq
  sigma12 = F.conv2d(img1 * img2, window, padding=window_size // 2, groups=channel) - mu1_mu2

  C1 = 0.01 ** 2
  C2 = 0.03 ** 2

  ssim_map = ((2 * mu1_mu2 + C1) * (2 * sigma12 + C2)) / ((mu1_sq + mu2_sq + C1) * (sigma1_sq + sigma2_sq + C2))

  if size_average:
      return ssim_map.mean()
  else:
      return ssim_map.mean(1).mean(1).mean(1)

PSNR（峰值信噪比）公式和作用

• PSNR 是一种评价图像质量的指标，用于衡量原始图像和重建图像之间的差异。
• 定义为：给定一个原始图像，另一个图像为重建图像，PSNR 就是原始图像和重建图像之间的均方误差 MSE 的平均值。
• 计算公式为：

  $$PSNR = 10 \log_{10} \frac{MAX_{I}^2}{MSE}$$

• 其中，MSE 是原始图像和重建图像之间的均方误差，MAX 是图像颜色的最大数值，8 位采样点表示为 255。

  $$MSE = \frac{1}{mn} \sum_{i=0}^{m-1} \sum_{j=0}^{n-1} ||I(i, j) - K(i, j)||^2$$

交叉熵 loss

• 交叉熵是信息论中的概念，用来衡量一个概率分布和另一个概率分布之间的距离。
• 在分类问题中，我们通常有一个真实的概率分布（训练数据的分布），以及一个模型生成的概率分布，交叉熵 keyi 衡量这两个分布之间的距离。
• 在模型训练时，通过最小化交叉熵损失函数，可以使模型预测的概率分布逐步接近真实的概率分布。
• 公式:

  $$L = -\frac{1}{N} \sum_{i=1}^{N} [y_i \log \hat{y}_i + (1-y_i) \log (1-\hat{y}_i)]$$

  交叉熵由来

  • 信息量：

    • 信息论中，信息量的表示方式：

      $$I(x_j) = -\ln p(x_j)$$

    • 即：概率越小的事件，信息量越大。

  • 熵：

    $$H(p) = -\sum_{j}^{n} p(x_j) \ln p(x_j)$$

  • 相对熵（KL 散度）：

    • 如果我们对于同一个随机变量$x$有两个单独的概率分布$p(x)$和$q(x)$，可以用 KL 散度衡量这两个分布之间的距离：

      $$D_{KL}(p||q) = \sum_{j=1}^n p(x_j) \ln \frac{p(x_j)}{q(x_j)}$$

    • n 为事件的所有可能性，D 的值越小，表示 q 分布和 p 分布越接近。

  • 交叉熵：

    • 把上述公式变形：

      $$\begin{aligned} D_{KL}(p||q) &= \sum_{j=1}^np(x_j)\ln p(x_j) - \sum_{j=1}^np(x_j)\ln q(x_j) \\ &= H(p, q) - H(p(x)) \end{aligned}$$

    • 其中，$H(p, q)$ 就是两个分布的交叉熵。

举例

• 假设N=3，期望输出为p=(1, 0, 0)，实际输出为q1 = (0.5, 0.2, 0.3)，q2 = (0.8, 0.1, 0.1)，那么交叉熵为：

  $$H(p, q1) = -(1 * ln0.5 + 0 * ln0.2 + 0 * ln0.3) = 0.693 \\ H(p, q2) = -(1 * ln0.8 + 0 * ln0.1 + 0 * ln0.1) = 0.223 \\$$

• q2的交叉熵更小，所以q2 分布更接近期望分布 p。

参考文档

• 交叉熵损失函数
• Deep Learning】L1 Loss、L2 Loss、Smooth L1 Loss