激活函数不以零为中心的问题

声明

• 本文转载自谈谈激活函数以零为中心的问题，非原创

神经元

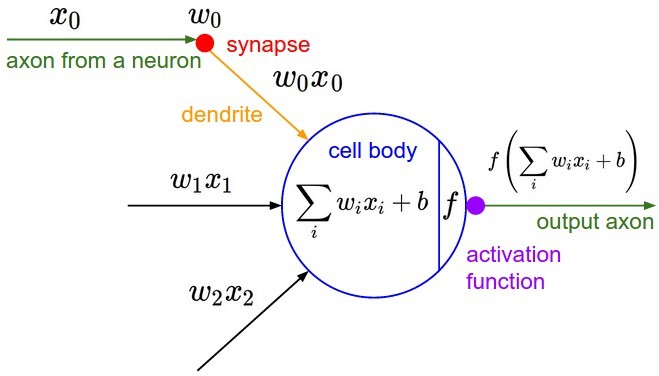
• 该神经元整合前一层神经元的消息为$z(\vec{x}, \vec{w}, \vec{b}) = \sum_i{w_ix_i+b}$，再送到激活函数$f(z)$。这里整合的过程是线性加权。

Sigmoid和tanh

• Sigmoid函数的一般形式为

$$\sigma(z) = \frac{1}{1+e^{-z}}$$

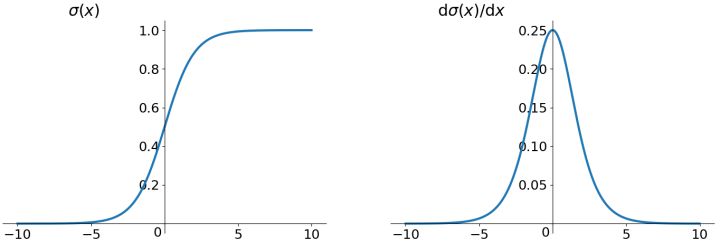
-tanh函数的一般形式为

$$tanh(z) = \frac{e^z - e^{-z}}{e^z + e^{-z}}$$

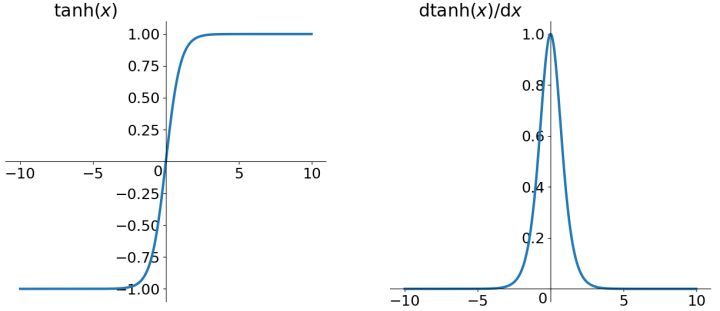
收敛速度

• 模型的最优解即是模型参数的最优解，通过多轮迭代，模型参数会被更新到接近最优解，这一过程，迭代次数越多，收敛速度越慢；反之，迭代次数越少，收敛速度越快。

参数更新

• 深度学习一般的学习方法是反向传播。简单来说，就是通过链式法则，求解全局损失函数$L(\vec{x})$对某一参数$w$的偏导数（梯度）；然后辅以学习率$\eta$，向梯度的反方向更新参数$w$。

$$w \leftarrow w-\eta \cdot \frac{\partial L}{\partial w}$$

• 考虑学习率$\eta$是全局设置的超参数，参数更新的核心步骤是计算$\frac{\partial L}{\partial w}$，再考虑到对于某个神经元来说，输入和输出的关系是：

$$f(\vec{x} ; \vec{w}, b)=f(z)=f\left(\sum_i w_i x_i+b\right) .$$

• 链式法则可以表示为：

$$\frac{\partial L}{\partial w_i}=\frac{\partial L}{\partial f} \frac{\partial f}{\partial z} \frac{\partial z}{\partial w_i}=x_i \cdot \frac{\partial L}{\partial f} \frac{\partial f}{\partial z} .$$

• 因此参数更新步骤变为：

$$w_i \leftarrow w_i-\eta x_i \cdot \frac{\partial L}{\partial f} \frac{\partial f}{\partial z} .$$

更新方向

• 由于$w_i$是上一轮迭代的结果，这里可以视为常数。因此参数$w_i$的更新方向是由$x_i \cdot \frac{\partial L}{\partial f} \frac{\partial f}{\partial z}$的符号决定的。

• 随便拿出来两个参数，他们的更新反向由以下关系决定：

$$\left\{\begin{matrix} x_i \cdot \frac{\partial L}{\partial f} \frac{\partial f}{\partial z}\\ x_j \cdot \frac{\partial L}{\partial f} \frac{\partial f}{\partial z} \end{matrix}\right.$$

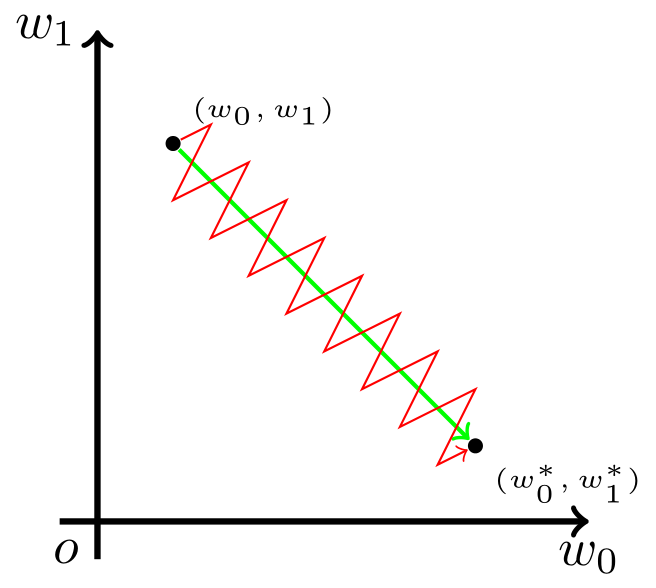
• 因此每个$w$更新方向，由此时的$x_i$的方向决定。假设当前情况下，$w_i$变小合适，$w_j$变大合适。但在Sigmoid函数中，输出值恒为正。也就是说如果上一级神经元采用Sigmoid函数作为激活函数，那么我们无法做到$x_i$和$x_j$方向相反。此时模型为了收敛，只能Z字形逼近最优解