2DGS学习笔记

相关文档

2DGS

• 项目链接：https://surfsplatting.github.io/
• 代码链接：https://github.com/hbb1/2d-gaussian-splatting
• 论文链接：https://arxiv.org/pdf/2403.17888
• 视频链接：
  • 新风向？——2DGS（2D 高斯泼溅）横空出世
  • 2D Gaussian Splatting 文章 + 代码串读（无敌详细/引经据典/疯狂解读）

Introduction

• 作者在 introduction 中介绍 3dgs 目前在捕捉复杂几何形状方面存在不足，因为其体积化的 3d 高斯模型和物体表面的薄片性质相冲突。
• 同时，历史已经有一些文章证明，surfels(surface elements)可以很好的表示复杂物体表面信息。并且在 SLAM 中也有一些基于 surfels 的 SLAM 算法。
• 3DGS 由于使用椭球体作为基础元素，是带有体积的。其是在光线和高斯椭球体相交的位置计算出一个"高斯值"，但当光线从不同位置射向椭球体时，这个其对应的深度信息是不一致的，这就无法渲染出准确且一致的深度信息。
• 作者提出自己的方法的优点：
  • 使用带有朝向信息的 2D 椭圆盘作为基础元素，利用显式射线散射交点，从而实现透视正确散射
  • 2D 高斯基本元素的表面法线可以直接通过法线约束进行表面平滑

• 总结一下，2DGS 方法的主要贡献：
  • 提出了一个高效的可微分 2D 高斯渲染器，通过利用 2D 表面建模、射线-高斯交点和体积积分实现了透视正确的 splatting
  • 引入了两个正则化损失项以改善和实现无噪声的表面重建，分别是深度失真和法线一致性

2DGS 方法

建模

• 2DGS 采用平坦的 2D 椭圆盘来表示稀疏点云，2D 基元将密度分布在平面圆盘上，并且定义法向量为密度变化最剧烈的方向（TODO：）。以下图为例：

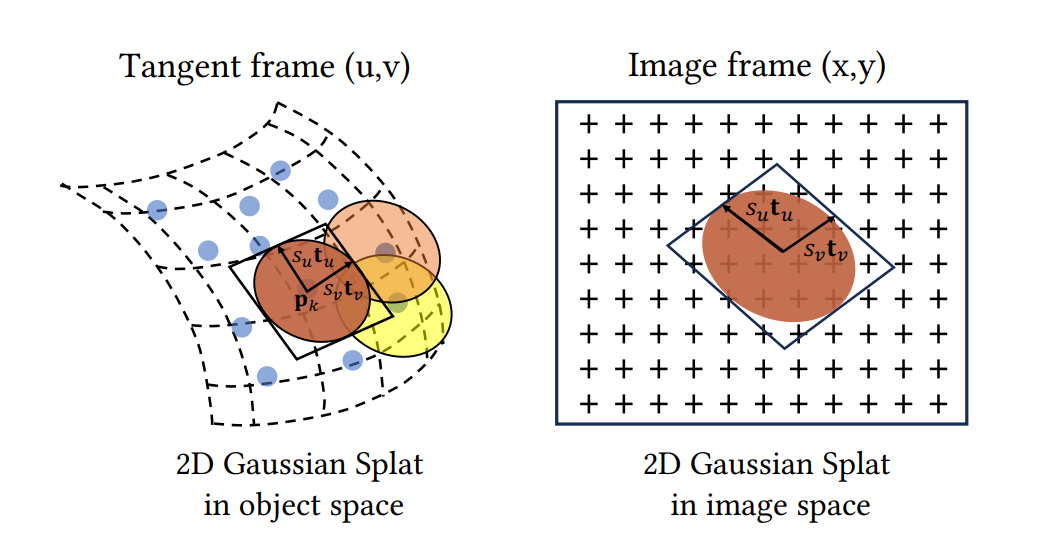
• 定义高斯的中心点为$\boldsymbol{p}_k$，两个主要切向量为$\boldsymbol{t}_u$和$\boldsymbol{t}_v$，以及缩放向量$\boldsymbol{S} = (s_u, s_v)$，利用以上信息可以定义一个 2D 高斯函数。其法向量由两个切向量叉乘得到$\boldsymbol{t}_w = \boldsymbol{t}_u \times \boldsymbol{t}_v$。此时，2D 高斯的朝向参数可以用旋转矩阵$\boldsymbol{R} = \begin{bmatrix}\boldsymbol{t}_u & \boldsymbol{t}_v & \boldsymbol{t}_w\end{bmatrix}$表示，缩放参数可以表示为最后一行为 0 的对角矩阵$\boldsymbol{S} = \begin{bmatrix}s_u & 0 & 0 \\ 0 & s_v & 0 \\ 0 & 0 & 0 \end{bmatrix}$。此时 2D 高斯函数可以表示为：

$$\begin{aligned} P(u, v) &= \boldsymbol{p}_k + s_u \boldsymbol{t}_u u + s_v \boldsymbol{t}_v v = H[u, v, 1 , 1]^T \\ where H &= \begin{bmatrix} s_u\boldsymbol{t}_u & s_v\boldsymbol{t}_v & \boldsymbol{0} & \boldsymbol{p}_k \\ 0 & 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} \boldsymbol{RS} & \boldsymbol{p}_k \\ \boldsymbol{0} & 1 \end{bmatrix} \end{aligned}$$

• 举个例子，假如有如下参数：
  • $\boldsymbol{p}_k = [1, 1, 1] \quad \boldsymbol{t}_u = [1, 0, 0] \quad \boldsymbol{t}_v = [0, 1, 0] \quad s_u = 2 \quad s_v = 3 \quad u = 0.5 \quad v = 0.5$
  • 则其对应在 3D 空间中的点坐标为：$P(u, v) = [1, 1, 1] + 2[1, 0, 0]*0.5 + 3[0, 1, 0]*0.5 = [2, 2.5, 1]$
• 同时，每个 2D 高斯还包含和 3D 高斯中一样的不透明度$\alpha$和与观察角度有关的，使用球谐函数表示的颜色$c$。
• 总结，一个 2D 高斯函数，有以下可学习的参数：
  • 2D 高斯中心点$\boldsymbol{p}_k$
  • 缩放参数$\boldsymbol{S} = (s_u, s_v)$
  • 朝向$[\boldsymbol{t}_u , \boldsymbol{t}_v]$
  • 不透明度$\alpha$
  • 颜色$c$（3 阶的话也是 16 个参数）

Splatting

• 3DGS 中，对透视投影做局部线性近似，来实现将 3D 投影到 2D 平面上，但这个方法只在中心点附近才准确，举例越远误差越大。
• 作者这里将 2D 的高斯投影到 image 上的过程，表示为齐次坐标系下的 2D-to-2D 的投影。定义$W\in 4 \times 4$为从世界坐标到屏幕空间的变换矩阵，则有：

$$\boldsymbol{x} = [xz, yz, z, 1]^T = W P(u, v) = WH(u, v, 1, 1)^T$$

• 屏幕空间：相机坐标系下的点，经过投影变换后的结果，是二维空间
• 其中，$\boldsymbol{x}$表示从位置$(x, y)$发射的一条齐次坐标表示的光线，其与 2D splat 在深度$z$处相交。根据上式，给定一个屏幕坐标$(x, y)$，可以通过$u = (WH)^{-1}\boldsymbol{x}$计算出像素坐标。但逆变换带来数值不稳定的问题，尤其是从侧面观察 splat 时，平面就退化为了一根线。为了解决这个问题，作者提出使用显式射线散射交点(ray-splat intersection)

ray-splat intersection：作者采用计算 3 个非平行平面的交点来得到 ray 和 splat 的交点。

1. 首先对于图像坐标$(x,y)$，定义两个正交平面$\boldsymbol{h}_x = [-1, 0, 0, x]^T$和$\boldsymbol{h}_y = [0, -1, 0, y]^T$，此时光线与 2D splat 的交点一定在这两个平面的交线上。
2. 将两个平面变换到 2D 高斯的局部坐标系下，根据前面的定义，$WH$为从 2D splat 的世界坐标系到屏幕空间的变换矩阵。且将一个点通过变换矩阵$M$变换的平面上等价于将使用$M^{-T}$变换平面的齐次参数，因此这里的$M = (WH)^{-1} = (WH)^T$。通过下式可以将两个正交平面变换到 2D 高斯局部坐标系下：

$$\boldsymbol{h}_u = (WH)^T \boldsymbol{h}_x \quad \boldsymbol{h}_v = (WH)^T \boldsymbol{h}_y$$

3. 前面定义过，2D 高斯平面的点定义为$(u, v, 1, 1)$，且交点一定落在这两个正交平面上，因此有：

$$\boldsymbol{h}_u = (u, v, 1, 1)^T = \boldsymbol{h}_v (u, v, 1, 1)^T = 0$$

4. 最终计算出 2D splat 局部坐标下的交点为：

$$u(\mathbf{x})=\frac{\mathbf{h}_u^2 \mathbf{h}_v^4-\mathbf{h}_u^4 \mathbf{h}_v^2}{\mathbf{h}_u^1 \mathbf{h}_v^2-\mathbf{h}_u^2 \mathbf{h}_v^1} \quad v(\mathbf{x})=\frac{\mathbf{h}_u^4 \mathbf{h}_v^1-\mathbf{h}_u^1 \mathbf{h}_v^4}{\mathbf{h}_u^1 \mathbf{h}_v^2-\mathbf{h}_u^2 \mathbf{h}_v^1}$$

• 其中$\boldsymbol{h}_u^i$表示 4D 齐次平面参数中第$i$个元素。

退化解 (Degenerate Solutions)

• 当二维高斯从倾斜角度观察时，在屏幕空间中可能会退化为一条线。这意味着在光栅化过程中，高斯分布可能会被忽略，从而导致渲染结果的精度降低。为了处理这种情况，论文引入了一个低通滤波器来稳定优化过程。具体方法如下：
  • 最大值滤波器：定义了一个新的高斯值$\hat{\mathcal{G}}(\mathrm{x})=\max \left\{\mathcal{G}(\mathbf{u}(\mathrm{x})), \mathcal{G}\left(\frac{\mathrm{x}-\mathbf{c}}{\sigma}\right)\right\}$，它取原始高斯值$\mathcal{G}(\mathbf{u}(x))$和低通滤波器值$\mathcal{G}\left(\frac{\mathbf{x}-\mathbf{c}}{\sigma}\right)$的最大值。这样可以确保即使在退化情况下，二维高斯分布仍然能被正确处理。
  • 其中, $u(\mathbf{x})$由上面的方程解给出，c 是中心$boldsymbol{p}_k$的投影。直观地说，$\hat{\mathcal{G}}(x)$由固定的屏幕空间高斯低通滤波器限定，该滤波器的中心为 ck 且半径为 σ，在实验中，作者设置$\sigma=\sqrt{2} / 2$以确保在渲染过程中使用足够的像素。

光栅化 (Rasterization)

• 与 3DGS 一样

训练

深度失真(Depth Distortion) loss

• 问题：当使用三维高斯分布进行渲染时，不同高斯分布可能会在深度上有交叠，这会导致渲染结果中的深度和颜色出现混乱，特别是在不同的高斯分布看起来很接近但实际上应该有不同深度时。
• 解决方案：引入深度失真正则化项，通过最小化交点之间的深度差距，来确保这些高斯分布在正确的深度位置上。这可以帮助集中权重分布，使得重建的几何形状更加清晰和准确。
  公式如下：

  $$\mathcal{L}_d=\sum_{i, j} \omega_i \omega_j\left|z_i-z_j\right|$$

法线一致性(Normal Consistency) loss

• 问题：在渲染过程中，如果二维高斯分布的法线（指向相机的方向）不一致，会导致表面不光滑，看起来不自然。特别是在处理半透明表面时，这个问题会更明显。
• 解决方案：引入法线一致性正则化项，通过对齐二维高斯分布的法线和实际表面的法线，确保重建的表面是光滑的，且局部几何形状准确。这意味着二维高斯分布的法线要与由深度图估计的表面法线一致。

结果对比

实测数据