机器学习相关基础概念

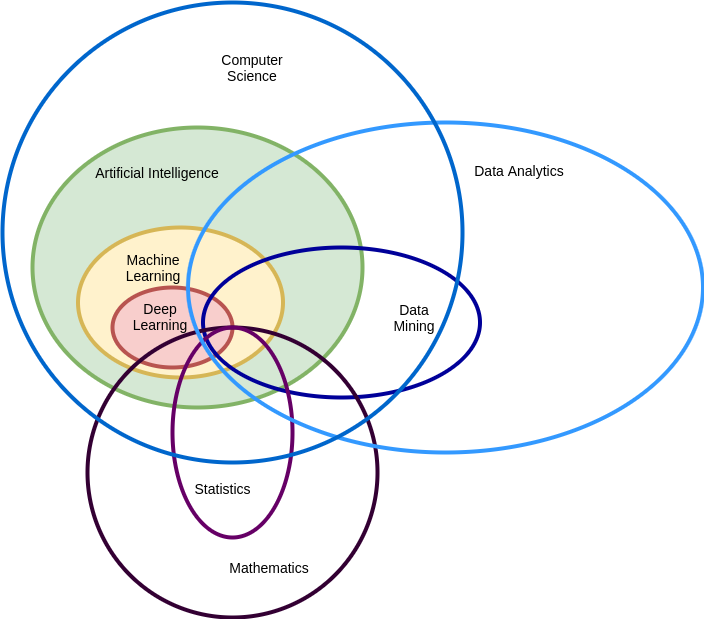
MLP

定义

• 多层感知机（Multilayer Perception, MLP）是一种基于前馈神经网络的深度学习模型，由多个神经元组成，其中每个神经元与前一层全连接。多层感知机可以用于解决分类、回归和聚类等任务。

• 多层感知机的每个神经元层由许多神经元组成，其中输入层接收输入特征，输出层给出最终的预测结果，中间的隐藏层用于提取特征和进行非线性变化。每个神经元接收前一层的输出，进行加权和激活函数运算，得到当前层的输出。通过不断迭代训练，多层感知机可以自动学习到输入特征之间的复杂关系，并对新的数据进行预测。

优缺点

优点

• 具有较强的表达能力，可以处理非线性问题和高位数据
• 可以通过反向传播算法进行训练，可以自动学习特征之间的复杂关系
• 可以处理多分类问题和回归问题，具有较好的泛化能力
• 可以添加正则项、dropout 来防止过拟合

缺点

• 需要大量的数据和计算资源，训练过程可能需要多次迭代
• 对初始权重和偏置的选择比较敏感，可能导致陷入局部最优解
• 对数据的标准化和预处理要求较高，需要进行归一化、标准化等预处理
• 模型难以解释

常用激活函数

GeLU(Gaussian error linear unit) 函数

ReLU (Rectified Linear Unit)函数

• 给定元素$x$，返回该元素和 0 的最大值

$$ReLU(x) = max(0, x)$$

• 它的导数为：

$$\frac{d}{dx}ReLU(x) = \begin{cases} 1, & x > 0 \\ 0, & x \leq 0 \end{cases}$$

Sigmoid 函数

• 将范围$(-\infty, \infty)$映射到$(0, 1)$，通常被称为挤压函数(squashing function)

$$sigmod(x) = \frac{1}{1 + e^{-x}}$$

• 它的导数为：

$$\frac{d}{dx}sigmoid(x) = \frac{e^{-x}}{(1+x^{-x})^2} = sigmoid(x)(1 - sigmoid(x))$$

Tanh 函数

• 将范围$(-\infty, \infty)$映射到$(-1, 1)$

$$tanh(x) = \frac{1 - e^{-2x}}{1 + e^{-2x}}$$

• 它的导数为：

$$\frac{d}{dx}tanh(x) = 1 - tanh^2(x)$$

Softmax

• Softmax计算的是一个比重，针对输出结果做归一化，将其映射到$[0, 1]$之间。

$$\frac{e^{z_k}}{\sum_{i=1}^{n}e^{z_i}}$$

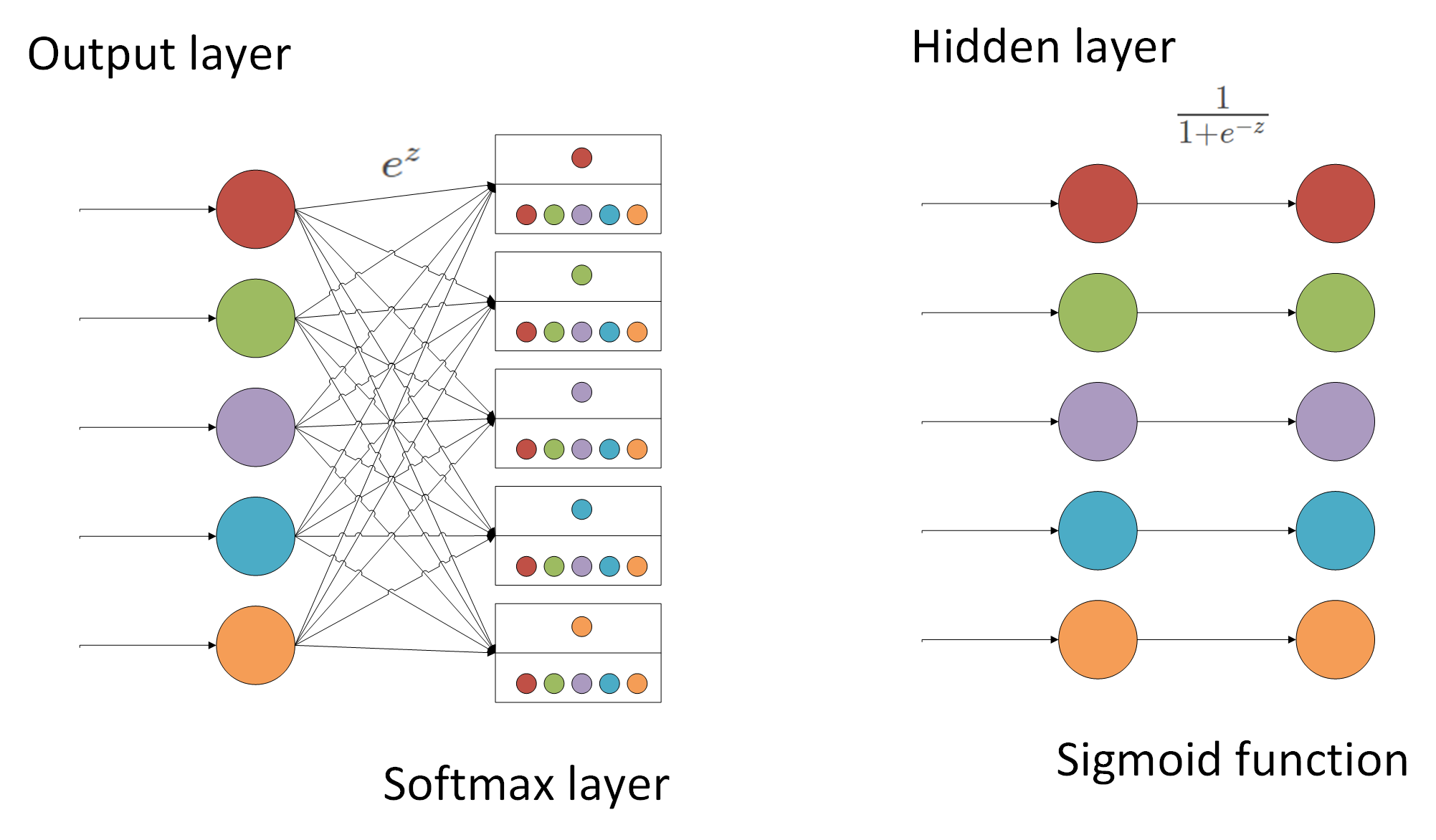
各自优缺点

• Sigmoid和Tanh是饱和函数，而ReLU是非饱和函数。
• 非饱和函数的优势有两点：
  • 梯度值稳定，不会因为函数饱和而梯度消失
  • 计算速度快，不需要进行指数运算

Sigmoid的缺点

• Sigmoid的单数都是小于0.25的，那么在进行反向传播时，梯度相乘的结果会慢慢趋近于0。这样几乎就没有梯度信号通过神经元传递到前面层的梯度更新中，这个时候前面层的权重几乎没有更新，这就会造成梯度消失。

• 输出不是零中心，所有神经元的w只能往一个方向走（一起变大或者一起变小，而不能一个变大一个变小），详细解释见：https://fansaorz.github.io/2024/12/14/激活函数不以零为中心的问题/

• 指数函数计算消耗资源

Tanh的优缺点

• 优点：解决了Sigmoid输出非零中心问题
• 缺点：梯度消失问题依然存在

ReLU的优缺点

• 优点：
  • 解决了梯度消失问题，至少x>0时，神经元不会饱和
  • 计算速度快
• 缺点：
  • 不是零中心
  • 存在神经元死亡问题，当x<0时，梯度为0

无监督学习和监督学习

无监督学习

• 训练数据集不包含标签数据。这意味着算法必须从数据中自己发现模式和结构。无监督学习可以用于聚类、降维和异常检测等问题。

监督学习

• 其训练数据集包括标签数据(也称为有监督数据)。这些标签数据告诉了机器学习算法输入数据与输出结果之间的对应关系。监督学习可以用于分类和回归问题，其中分类问题是对输入数据进行分类，回归问题是对输入数据进行连续值的预测。

自监督学习

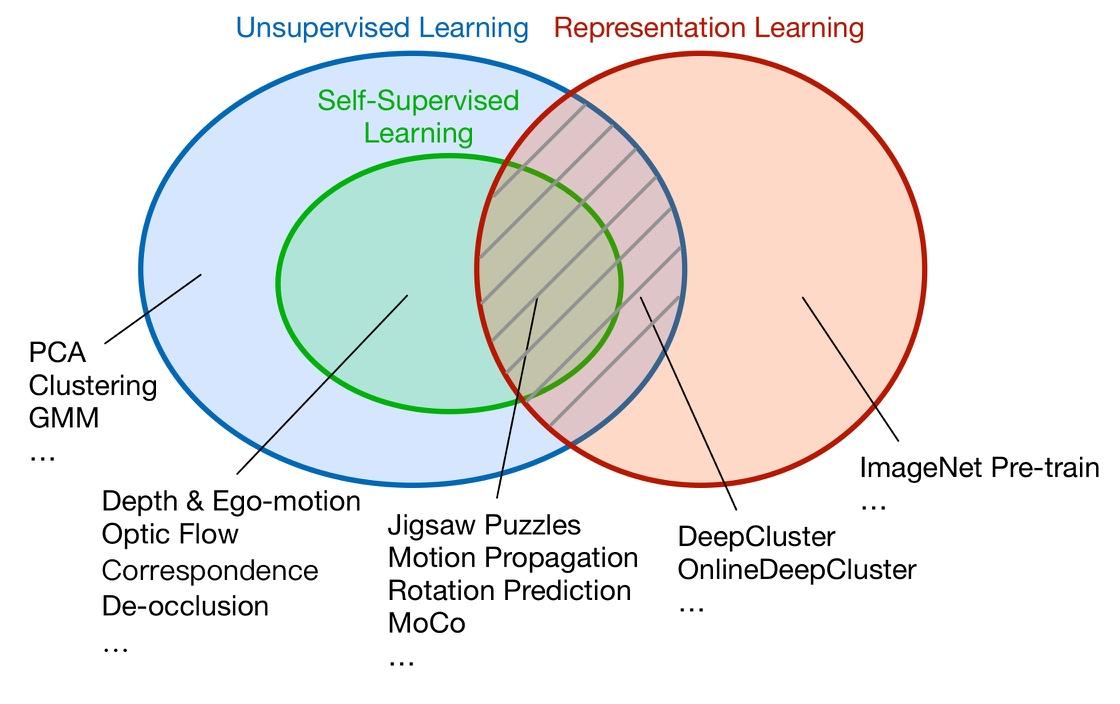
• 自监督学习是指用于机器学习的的标注，来自于数据本身，而不是人工标注。如下图，自监督学习首先属于无监督学习，因此其学习的目标无需人工标注。

• 目前自监督学习领域可以大致分为两个分支。

  • 第一是用于解决特定任务的自监督学习，例如：自监督的深度估计、光流估计、图像关联点匹配等。
  • 第二个是用于表征学习，例如：运动传播，旋转预测等

分类、回归、聚类

分类（Classification）

• 分类任务是将输入数据划分为不同的类别。属于监督学习领域，因为要使其发挥作用，必须通过使用正确标记的记录示例，来引导它。在完成对计算机的训练后，您可以对新记录测试，进行评分，并查看其准确程度。
• 举例：
  • 垃圾邮件分类
  • 图像识别

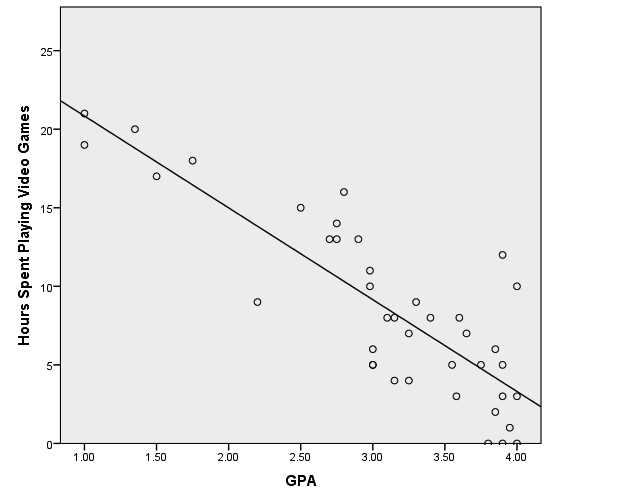
回归（Regression）

• 回归的目标是预测许多样本中，相关(要素/特征)的连续值。连续值意味着输入的微小变化，导致输出的微小变化。属于监督学习领域，因为必须提供标记样本，然后尝试搞出一个拟合到样本特征的方程
• 举例：
  • 预测房价
  • 预测股票价格

聚类（Clustering）

• 聚类的目标是，自动将类似的样本分组。由于聚类算法不具备如何定义集合的任何先验知识，因此它是一个无监督学习任务。需要有一种方法来判断哪些样本是相似的，并自动将它们分组。它与人类的思维方式相似，通过查看各个样本的特征和要素，来识别相似性。
• 举例：
  • 客户细分
  • 根据个人资料，在婚恋网站上匹配相似的人

正则化（Regularization）

损失函数

Softmax

优化器

模型评估

交叉验证

偏差和方差

卷积层

池化层

Dropout

正向传播

反向传播

梯度下降

梯度消失和梯度爆炸

学习率

参考文档：

• 《动手学深度学习》

• https://www.itheima.com/news/20230309/113041.html

• https://llever.com/pass-blog/2019/04/22/数据科学之五大问题类降维分类聚类强化回归/

• https://blog.csdn.net/JasonH2021/article/details/131021534

• 自监督学习的一些思考